Алгебраические уравнения, разрешимые в гипергеометрических функциях (Лахтин)/Глава IV/ДО

Алгебраическiя уравненiя, разрѣшимыя въ гипергеометрическихъ функцiяхъ — Глава IV. Конечныя группы линейныхъ подстановокъ
авторъ Л. К. Лахтинъ

§ 13. Общіе пріемы вычисленія подстановокъ группы, соотвѣтствующей данной сѣти треугольниковъ  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

730

§ 14. Геометрическія представленія для группъ конечныхъ порядковъ  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

736

§ 15. Группа двупирамидная  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

743

§ 16. Группа тетраэдрическая  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

746

§ 17. Группа октаэдрическая  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

753

§ 18. Группа икосаэдрическая  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

758

§ 19. Циклическая группа конечнаго порядка  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

762

§ 20. Конечныя группы бинарныхъ линейныхъ подстановокъ  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

764

---

Глава IV.

Конечныя группы линейныхъ подстановокъ.

§ 13. Общіе пріемы вычисленія подстановокъ группы, соотвѣтствующей данной сѣти треугольниковъ.

Пусть дана сѣть треугольниковъ. Соединивъ треугольники попарно, мы получимъ сѣть четыреугольниковъ. Каждый изъ этихъ четыреугольниковъ есть основная область нѣкоторой неизвѣстной намъ группы линейныхъ подстановокъ. Всѣ четыреугольники эквивалентны между собою относительно подстановокъ этой группы.

Для краткости мы будемъ обозначать четыреугольники сѣти нумерами: $1,\ 2,\ 3\ldots .$

Черт. 18^[1]Возьмемъ въ четыреугольникѣ 1-мъ произвольную точку $u_{1}$ (черт. 18), строимъ рядъ зеркальныхъ изображеній точки $u_{1}$:

$u'_{1},\ u_{1},\ u'_{2},\ u'_{3}\ldots$

‎Въ каждомъ четыреугольникѣ найдется по одной точкѣ, соотвѣтствующей точкѣ $u_{1}$:

$u_{1},\ u_{2},\ u_{3}\ldots$

‎Точки $u'_{1},\ u'_{2},\ u'_{3}\ldots$ будутъ симметричны съ точками $u_{1},\ u_{2},\ u_{3}\ldots$ относительно діагоналей четыреугольниковъ.

Теорема 1. Стороны четыреугольника сѣти попарно эквивалентны.

Будемъ двигать точку $u_{1}$ внутри четыреугольника 1, приближая ее къ какой нибудь точкѣ $e$ стороны $ad$. Зеркальное изображеніе $u'_{1}$ будетъ приближаться къ точкѣ $e'$, симметричной съ точкой $e$ относительно діагонали $bd$. Точка $u_{2}$, симметричная съ $u'_{1}$ относительно стороны $cd$, будетъ приближаться къ той же точкѣ $e'$ стороны $cd$. Въ тотъ моментъ, когда $u_{1}$ придетъ въ $e$, точка $u_{2}$ придетъ въ $e'$.

Точки $u_{1}$ и $u_{2}$ суть точки соотвѣтственныя въ четыреугольникахъ 1 и 2. Онѣ связаны между собою линейной подстановкой $S$, преобразующей четыреугольникъ 1 въ четыреугольникъ 2:

$u_{2}=S(u_{1}).$

(1)

‎Если такъ, то:

$e'=S(e).$

(2)

‎Это послѣднее равенство справедливо, гдѣ бы на сторонѣ $ad$ мы ни взяли точку $e$: сторона $ad$ эквивалентна сторонѣ $cd$, и подстановка, преобразующая $ad$ въ $cd$, есть та подстановка $S$, которая преобразуетъ четыреугольникъ 1 въ 2.

Будемъ двигатъ точку $u_{1}$, приближая ее къ какой нибудь точкѣ $f$ стороны $ab$. Зеркальное изображеніе $u'_{1}$ будетъ приближаться къ точкѣ $f'$, симметричной съ $f$ относительно діагонали $bd$. Точка $u_{4}$, симметричная съ $u'_{1}$ относительно стороны $bc$, будетъ приближаться къ той же точкѣ $f'$ стороны $bc$. Въ тотъ моментъ, когда точка $u_{1}$ придетъ въ $f$, точка $u_{4}$ придетъ въ $f'$. Точки $u_{1}$ и $u_{4}$ суть соотвѣтственныя точки въ четыреугольникахъ 1 и 4; онѣ связаны между собою линейной подстановкой ${\mathfrak {T}}$, преобразующей четыреугольникъ 1 въ 4:

$u_{4}={\mathfrak {T}}(u_{1}).$

(3)

‎Если такъ, то:

$f'={\mathfrak {T}}(f).$

(4)

‎Это равенство справедливо, гдѣ бы на сторонѣ $ab$ мы ни взяли точку $f$: сторона $cb$ эквивалентна сторонѣ $ab$ и подстановка, преобразующая $ab$ въ $cb$, есть та подстановка ${\mathfrak {T}}$, которая преобразуетъ четыреугольникъ 1 въ 4.

Четыреугольникъ 1 былъ взятъ совершенно произвольно; поэтому мы въ правѣ сказать, что стороны всякаго четыреугольника сѣти попарно эквивалентны^[2].

Теорема доказана.

Слѣдуя Пуанкаре, будемъ называть эквивалентныя стороны четыреугольника сопряженными.

Для послѣдующаго важно обратить вниманіе на слѣдующее обстоятельство.

Подстановка $S^{-1}$, преобразующая сторону $cd$ въ сопряженную съ ней $ad$, есть та подстановка, которая преобразуетъ четыреугольникъ 1 въ 3^[3]; слѣдовательно подстановка, преобразующая четыреугольникъ 1 въ 2, обратна той, которая преобразуетъ четыреугольникъ 1 въ 3.

На томъ же основаніи подстановка, преобразующая четыреугольникъ 1 въ 4, обратна той, которая преобразуетъ четыреугольникъ 1 въ 5.

Эти послѣднія заключенія мы можемъ формулировать въ видѣ теоремы:

Теорема 2. Подстановки, преобразующія четыреугольникъ 1 въ смежные, суть:

$S,\ {\mathfrak {T}},\ S^{-1},\ {\mathfrak {T}}^{-1}.$

(5)

‎Теорема 3. Подстановки:

$S$ и ${\mathfrak {T}}$

‎суть основныя^[4] подстановки группы.

Возьмемъ четыреугольникъ 1-ый и какой нибудь четыреугольникъ $m$-ый данной сѣти и въ нихъ отмѣтимъ соотвѣтственныя точки $u_{1}$ и $u_{m}$. Пусть четыреугольникъ $m$-ый получается изъ четыреугольника 1-го линейнымъ преобразованіемъ $\Sigma$:

$u_{m}=\Sigma (u_{1}).$

(6)

‎Будемъ точку $u_{m}$ перемѣщать такъ, чтобы она вышла изъ четыреугольника $m$-го, вступила въ смежный съ нимъ четыреугольникъ $m+1$-ый и пришла въ совпаденіе съ точкой $u_{m+1}$ этого послѣдняго четыреугольника, при чемъ подъ $u_{m+1}$ мы подразумѣваемъ точку четыреугольника $m+1$-го, эквивалентную $u_{1}$ относительно подстановокъ группы. Въ то же время точка $u_{1}$ будетъ, необходимо, также перемѣщаться, выйдетъ изъ четыреугольника 1-го и вступитъ въ одинъ изъ смежныхъ съ нимъ четыреугольниковъ. Для опредѣленности положимъ, что она вступила въ четыреугольникъ 2-ой.

Въ тотъ моментъ, когда точка $u_{m}$ пришла въ $u_{m+1}$, точка $u_{1}$ достигнетъ $u_{2}$.

Ясно, что точки $u_{m+1}$ и $u_{2}$ связаны между собою подстановкою $\Sigma$:

$u_{m+1}=\Sigma (u_{2}).$

(7)

‎Подставивъ въ это равенство вмѣсто $u_{2}$ ея выраженіе:

$u_{2}=S(u_{1}),$

(1)

‎находимъ:

$u_{m+1}=\Sigma S(u_{1}).$

(8)

‎Это значитъ, что четыреугольникъ $m+1$-ый, смежный съ четыреугольникомъ $m$-мъ, получается изъ четыреугольника 1-го подстановкой:

$\Sigma S.$

(9)

‎На основаніи тѣхъ же разсужденій мы въ правѣ сказать, что остальные три четыреугольника, смежные съ $m$-мъ, получаются изъ четыреугольника 1-го подстановками:

$\Sigma {\mathfrak {T}},\ \Sigma S^{-1},\ \Sigma {\mathfrak {T}}^{-1}.$

(10)

‎Итакъ, если четыреугольникъ $m$-ый получается изъ начальнаго четыреугольника 1-го подстановкой $\Sigma$, то четыреугольники, смежные съ $m$-мъ, получаются изъ 1-го подстановками:

$\Sigma S,\ \Sigma S^{-1},\ \Sigma {\mathfrak {T}},\ \Sigma {\mathfrak {T}}^{-1}.$

(11)

‎Пользуясь этимъ результатомъ, мы можемъ найти подстановку, преобразующую четыреугольникъ 1-ый въ любой четыреугольникъ сѣти. Въ самомъ дѣлѣ, въ теоремѣ 2 мы видѣли, что четыреугольники, смежные съ 1-мъ, получаются изъ него подстановками:

$S,\ {\mathfrak {T}},\ S^{-1},\ {\mathfrak {T}}^{-1}.$

(5)

‎Отсюда слѣдуетъ, что четыреугольники, смежные съ только что перечисленными, получаются изъ четыреугольника 1-го подстановками:

$\left.{\begin{array}{l}S^{2},\ S{\mathfrak {T}},\ S{\mathfrak {T}}^{-1},\\{\mathfrak {T}}S,\ {\mathfrak {T}}^{2},\ {\mathfrak {T}}S^{-1},\\S^{-1}{\mathfrak {T}},\ S^{-2},\ S^{-1}{\mathfrak {T}}^{-1},\\{\mathfrak {T}}^{-1}S,\ {\mathfrak {T}}^{-1}S^{-1},\ {\mathfrak {T}}^{-2}.\end{array}}\right\}.$

(12)

‎Имѣя подстановки (5) и (12), мы найдемъ подстановки, соотвѣтствующія слѣдующимъ четыреугольникамъ, смежнымъ съ разсмотрѣнными, и т. д. Такъ, мы найдемъ подстановки, соотвѣтствующія всѣмъ четыреугольникамъ сѣти. Всѣ эти подстановки будутъ представляться формулами вида:

$S^{\alpha }\ {\mathfrak {T}}^{\beta }\ S^{\gamma }\ {\mathfrak {T}}^{\delta }\ \ldots \ S^{\varkappa }\ {\mathfrak {T}}^{\lambda },$

(13)

‎гдѣ $\alpha ,\ \beta ,\ \gamma ,\ \delta ,\ \ldots ,\ \varkappa ,\ \lambda$ суть числа цѣлыя положительныя или отрицательныя. Нѣкоторыя изъ нихъ могутъ равняться нулю.

Итакъ, мы доказали, что всякая подстановка группы можетъ быть составлена изъ подстановокъ $S$ и ${\mathfrak {T}}$. Остается доказать, что эти подстановки $S$ и ${\mathfrak {T}}$ независимы между собою.

Допустимъ, что подстановки $S$ и ${\mathfrak {T}}$ не независимы. Въ такомъ случаѣ одна изъ нихъ должна быть степенью другой. Пусть:

${\mathfrak {T}}=S^{\alpha }.$

(14)

‎Подстановка $S$, какъ мы видѣли, преобразуетъ сторону $da$ четыреугольника 1 въ сопряженную съ нею сторону $dc$; при этомъ точка $d$ преобразуется сама въ себя.

Слѣдовательно, точка $d$ есть одна изъ двухъ точекъ, не мѣняемыхъ подстановкою $S$. Если точка $d$ не мѣняется подстановкою $S$, то она не можетъ мѣняться и подстановкой:

${\mathfrak {T}}=S^{\alpha }.$

(14)

‎Между тѣмъ мы знаемъ, что подстановка ${\mathfrak {T}}$ преобразуетъ четыреугольникъ 1 въ четыреугольникъ 4, не прилегающій ни къ сторонѣ $ad$, ни къ сторонѣ $dc$. Слѣдовательно, точка $d$ подстановкою ${\mathfrak {T}}$ непремѣнно мѣняется.

Такое противорѣчіе произошло отъ сдѣланнаго нами допущенія, что подстановки ${\mathfrak {T}}$ и $S$ не независимы между собою.

Итакъ, дѣйствительно, подстановки $S$ и ${\mathfrak {T}}$ суть основныя подстановки группы.

Если бы, какъ мы допустили выше, подстановка ${\mathfrak {T}}$ была зависима отъ $S$, то группа была бы циклическая:

$S^{0}=1,\ S,\ S^{2},\ S^{3}\ldots$

(15)

‎Основною областью такой группы не служитъ четыреугольникъ. О циклической группѣ конечнаго порядка мы будемъ говорить въ § 19 и увидимъ, что основною областью ея служитъ двуугольникъ, образованный дугами круговъ^[5].

Посмотримъ теперь, какъ по данной сѣти четыреугольниковъ построить соотвѣтствующую ей группу линейныхъ подстановокъ.

Примемъ одинъ изъ четыреугольниковъ сѣти за основной четыреугольникъ. Діагональною дугою окружности онъ дѣлится на два треугольника, изъ которыхъ одинъ бѣлый, а другой черный. Стороны четыреугольника, симметричныя относительно этой діагонали, суть сопряженныя. Найдемъ линейныя подстановки $S$ и ${\mathfrak {T}}$ преобразующія двѣ стороны четыреугольника въ двѣ другія стороны, сопряженныя съ ними.

Эти подстановки $S$ и ${\mathfrak {T}}$ суть основныя подстановки группы.

Имѣя основныя подстановки, мы можемъ указаннымъ выше способомъ найти подстановку, соотвѣтствующую каждому четыреугольнику сѣти. При этомъ особенности данной сѣти могутъ значительно облегчить вычисленія.

Такъ, напримѣръ, вычисленія значительно упростятся, если намъ удастся найти эллиптическую подстановку и извѣстенъ уголъ соотвѣтствующаго ей поворота сферы.

Во всѣхъ случаяхъ, съ которыми намъ придется встрѣтиться, всѣ подстановки будутъ эллиптическія и вычисленія совершаются очень легко. Поэтому мы не будемъ останавливаться на этихъ вычисленіяхъ и только на чертежахъ будемъ отмѣчать подстановки, соотвѣтствующія каждому четыреугольнику.

§ 14. Геометрическія представленія для группъ конечныхъ порядковъ.

Вообразимъ вписанный въ сферу одинъ изъ многогранниковъ, указанныхъ въ § 12, соотвѣтствующую ему сѣть на сферѣ и ея стереографическую проэкцію на плоскость.

Такъ какъ всѣ подстановки группы, соотвѣтствующей этой сѣти,—конечнаго порядка, то всѣ онѣ эллиптическія. Онѣ соотвѣтствуютъ такимъ поворотамъ сферы около центра, которые приводятъ сѣть на сферѣ и вписанный многогранникъ въ ихъ прежнее положеніе. Ясно, что эти повороты могутъ происходить около осей, проходящихъ или 1) черезъ вершину многогранника, или 2) черезъ центръ его грани, или 3) черезъ средину ребра. Въ первомъ случаѣ поворотъ совершается на уголъ ${\frac {2\pi }{\lambda }}$, гдѣ $\lambda$ число граней многогранника, сходящихся около вершины, во второмъ случаѣ поворотъ совершается на уголъ ${\frac {2\pi }{3}}$, въ третьемъ случаѣ—на уголъ $\pi$. Порядокъ подстановки, соотвѣтствующей повороту, равенъ въ первомъ случаѣ $\lambda$, во второмъ—числу 3 въ третьемъ—числу 2.

Будемъ называть для краткости проэкціи на поверхность сферы центровъ граней и срединъ реберъ многогранника—центрами граней, срединами реберъ.

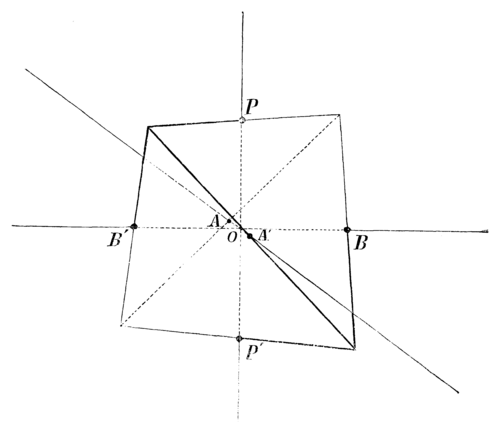
Черт. 19Изъ числа группъ двупирамиднаго типа намъ больше всего придется имѣть дѣло съ группой 4-го порядка, такъ называемой четверичной группой (Vierergruppe по Клейну). Многогранникъ, соотвѣтствующій четверичной группѣ, есть четырехгранная двупирамида. Ясно, что мы называемъ ее многогранникомъ лишь ради аналогіи: она имѣетъ видъ четыреугольника $APA'P'$, вписаннаго въ сферу (черт. 19). Точки $P$ и $P'$ мы разсматриваемъ, какъ вершины четырехгранной двупирамиды, $A$ и $A'$ какъ вершины основанія ея, а точки $B$ и $B'$, лежащія на перпендикулярѣ $BB'$ къ плоскости $APA'P'$—какъ средины реберъ основанія четырехгранной двупирамиды.

Ниже, на черт. 26, изображена четверичная сѣть, соотвѣтствующая четырехгранной двупирамидѣ, изображенной на черт. 19.

Сравнимъ между собою расположенія вершинъ, центровъ граней и срединъ реберъ для четырехъ видовъ многогранниковъ: четырехгранной двупирамиды, тетраэдра, октаэдра и икосаэдра.

Помѣстимъ тетраэдръ въ сферѣ такъ, чтобы средины реберъ его находились на осяхъ координатъ, къ которымъ отнесена сфера. Такое положеніе его изображено на черт. 20.

Ясно, что средины реберъ его: $A',\ P,\ A,\ P'$ могутъ быть приняты за вершины четырехгранной двупирамиды; шесть срединъ граней тетраэдра распадаются на три группы точекъ, изъ которыхъ каждая группа можетъ быть принята за вершины четырехгранной двупирамиды. Это мы выразимъ словами:

Черт. 20

‎тетраэдру соотвѣтствуетъ три четырехгранныхъ двупирамиды. Обратно: четырехгранной двупирамидѣ соотвѣтствуетъ одинъ опредѣленный тетраэдръ.

Каждый поворотъ, соотвѣтствующій подстановкѣ четверичной группы, приводитъ какъ четырехгранную двупирамиду, такъ и тетраэдръ въ прежнее ихъ положеніе, но не обратно: нѣкоторые повороты тетраэдрической группы будутъ смѣнять между собою три четырехгранныя двупирамиды, соотвѣтствующія тетраэдру.

Отсюда заключаемъ, что въ тетраэдрической группѣ заключаются три четверичныя группы.

Помѣстимъ октаэдръ въ сферѣ такъ, чтобы вершины его лежали на осяхъ координатъ. Такое положеніе его изображено на черт. 21.

Черт. 21

Мы видимъ, что вершины его совпадаютъ съ срединами реберъ тетраэдра, изображеннаго на черт. 20.

Изъ числа восьми центровъ граней октаэдра четыре совпадаютъ съ вершинами, а остальныя четыре съ центрами граней тетраэдра.

Октаэдру соотвѣтствуютъ два взаимно дополнительныхъ тетраэдра, изъ которыхъ одинъ переходитъ въ другой при поворотѣ на уголъ ${\frac {\pi }{2}}$ около каждой изъ трехъ осей, соединяющихъ противоположныя вершины октаэдра. Обратно, тетраэдру соотвѣтствуетъ вполнѣ опредѣленный октаэдръ.

Отсюда слѣдуетъ, что повороты, соотвѣтствующіе подстановкамъ тетраэдрической группы, не мѣняютъ положенія октаэдра, но не обратно: нѣкоторые повороты октаэдрической группы смѣняютъ между собою два тетраэдра, соотвѣтствующихъ октаэдру.

Отсюда заключаемъ, что въ октаэдрическую группу входятъ двѣ тетраэдрическія.

Помѣстимъ, наконецъ, икосаэдръ въ сферѣ такъ, чтобы шесть срединъ реберъ его лежали на осяхъ координатъ. Такое положеніе его изображено на черт. 22.

Черт. 22

Средины реберъ икосаэдра, лежащія на осяхъ координатъ, могутъ быть приняты за вершины октаэдра. Всѣ 30 срединъ реберъ икосаэдра распадаются на 5 группъ по 6 точекъ въ каждой, при чемъ 6 точекъ каждой такой группы могутъ служить вершинами октаэдра.

Слѣдовательно, икосаэдру соотвѣтствуетъ 5 октаэдровъ. Однако необходимо замѣтить, что каждому октаэдру соотвѣтствуетъ 2 икосаэдра: повернувъ октаэдръ на уголъ ${\frac {\pi }{2}}$ около какой либо оси, соединяющей двѣ его противоположныя вершины, мы измѣнимъ положеніе соотвѣтствующаго ему икосаэдра: переведемъ его изъ положенія, изображеннаго на черт. 22 въ положеніе, изображенное на черт. 23.

Черт. 23

Слѣдовательно октаэдрическая группа не входитъ въ составъ икосаэдрической.

Возьмемъ снова икосаэдръ, изображенный на чертежѣ 22. Средины реберъ его, лежащія на осяхъ координатъ, могутъ быть приняты за средины реберъ тетраэдра. Такъ какъ каждому октаэдру соотвѣтствуетъ два взаимно дополнительныхъ тетраэдра, то икосаэдру соотвѣтствуетъ 5 паръ взаимно дополнительныхъ тетраэдровъ. Каждый поворотъ, не мѣняющій положеніе одного изъ этихъ тетраэдровъ, не измѣнитъ ни положенія дополнительнаго ему тетраэдра, ни положенія икосаэдра. Каждому тетраэдру соотвѣтствуетъ одинъ опредѣленный икосаэдръ.

Изъ сказаннаго слѣдуетъ, что въ икосаэдрическую группу входитъ 5 группъ тетраэдрическихъ.

Помѣстимъ икосаэдръ въ сферѣ такъ, чтобы одна изъ осей, соединяющихъ двѣ противоположныя вершины его, совпала съ осью сферы, а одна изъ плоскостей симметріи, проходящихъ черезъ эту ось, прошла черезъ дѣйствительную ось плоскости перемѣннаго $u$. Такое положеніе икосаэдра изображено на черт. 24.

Въ послѣдующихъ вычисленіяхъ намъ понадобится выраженіе линейной подстановки, соотвѣтствующей тому повороту сферы, который приводитъ икосаэдръ изъ положенія, изображеннаго на черт. 22, въ положеніе, изображенное на черт. 24.

Полюсами оси вращенія въ данномъ случаѣ служатъ точки $+i$ и $-i$. Вращеніе происходитъ около оси $AA'$ (черт. 22) въ положительномъ направленіи относительно наблюдателя, смотрящаго отъ $A$ къ $A'$. Уголъ поворота $\theta$ отмѣченъ на чертежѣ 22 и опредѣляется формулою:

$tg\,\theta ={\frac {1}{2cos\,36^{\circ }}}.$

(16)

‎Примѣняя формулы (39) и (41) главы III, находимъ, что искомая подстановка $\sigma$ выражается такъ:

$\sigma (u)={\frac {u+tg\,{\dfrac {\theta }{2}}}{u\,tg\,{\dfrac {\theta }{2}}-1}}.$

(17)

‎Обратная ей подстановка такова:

$\sigma ^{-1}(u)={\frac {u-tg\,{\dfrac {\theta }{2}}}{u\,tg\,{\dfrac {\theta }{2}}+1}}.$

(18)

Черт. 24

§ 15. Группа двупирамидная.

Углы треугольника двупирамидной группы суть: ${\frac {\pi }{m}},\ {\frac {\pi }{2}},\ {\frac {\pi }{2}}$, гдѣ $m$ произвольное цѣлое число^[6].

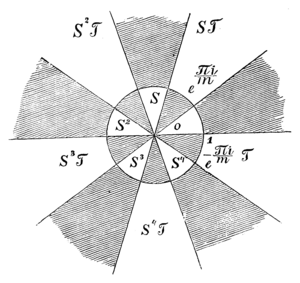Черт. 25Помѣстимъ двупирамиду въ сферѣ такъ, чтобы ось ея совпала съ осью сферы и чтобы двѣ вершины основанія ея лежали симметрично относительно положительнаго направленія дѣйствительной оси. Тогда сѣть представляется въ такомъ видѣ, какъ изображено на черт. 25 (чертежъ этотъ соотвѣтствуетъ случаю $m=5$).

Условимся называть сѣть 25 нормальною двупирамидною сѣтью, соотвѣтствующую ей группу — нормальною двупирамидною группой.

Примемъ четыреугольникъ $0e^{-{\frac {\pi i}{m}}}1e^{\frac {\pi i}{m}}$ за основной четыреугольникъ сѣти.

Сопряженныя стороны его суть: $0e^{-{\frac {\pi i}{m}}}$ и $0e^{\frac {\pi i}{m}}$, $1e^{-{\frac {\pi i}{m}}}$ и $1e^{\frac {\pi i}{m}}$.

Возьмемъ какую нибудь точку $u$ на сторонѣ $0e^{-{\frac {\pi i}{m}}}$ и соотвѣтствующую ей точку $u'$ на сторонѣ $0e^{\frac {\pi i}{m}}$. Ясно, что

$u=\rho e^{-{\frac {\pi i}{m}}},\ u'=\rho e^{\frac {\pi i}{m}},$ гдѣ $0<\rho <1.$

‎Отсюда:

$u'=\varepsilon u,$ гдѣ $\varepsilon =e^{\frac {2\pi i}{m}}.$

(19)

‎Подстановка $S$, преобразующая сторону $0e^{-{\frac {\pi i}{m}}}$ въ сопряженную съ нею сторону $0e^{\frac {\pi i}{m}}$, выражается такъ:

$S(u)=\varepsilon u,$ гдѣ $\varepsilon =e^{\frac {2\pi i}{m}}.$

(20)

‎Возьмемъ точку $u$ на сторонѣ $1e^{-{\frac {\pi i}{m}}}$ и соотвѣтствующую ей точку $u'$ на сторонѣ $1e^{\frac {\pi i}{m}}$. Ясно, что

$u=e^{-\psi i},\ u'=e^{\psi i},$ гдѣ $0<\psi <{\frac {\pi i}{m}}.$

‎Отсюда:

$u'={\frac {1}{u}}.$

(21)

‎Подстановка ${\mathfrak {T}}$, преобразующая сторону $1e^{-{\frac {\pi i}{m}}}$ въ сопряженную съ нею сторону $1e^{\frac {\pi i}{m}}$, выражается такъ:

${\mathfrak {T}}(u)={\frac {1}{u}}.$

(22)

‎Для отличія символовъ подстановокъ двупирамидной группы отъ символовъ иныхъ подстановокъ, мы присоединимъ къ этимъ символамъ индексъ «д» (двупирамида).

Итакъ, основныя подстановки двупирамидной группы таковы:

$\left.{\begin{array}{l}S_{\text{д}}(u)=\varepsilon u,\ {\text{гдѣ}}\ \varepsilon =e^{\frac {2\pi i}{m}},\\{\mathfrak {T}}_{\text{д}}(u)={\dfrac {1}{u}}.\end{array}}\right\}$[7]

(23)

‎Первая изъ нихъ $m$-го порядка, а вторая—2-го порядка.

Первая изъ нихъ соотвѣтствуетъ повороту сферы на уголъ ${\frac {2\pi }{m}}$ около оси, соединяющей полюсы сферы, а вторая—повороту сферы на уголъ $\pi$ около дѣйствительной оси.

Вся совокупность $2m$ подстановокъ нормальной двупирамидной группы исчерпывается слѣдующими формулами:

${\begin{matrix}\left.{\begin{array}{l}S_{\text{д}}^{k}(u)=\varepsilon ^{k}u,\\S_{\text{д}}^{k}{\mathfrak {T}}_{\text{д}}={\dfrac {\varepsilon ^{k}}{u}},\end{array}}\right\}&{\text{ гдѣ: }}&{\begin{array}{l}k=0,\ 1,\ 2,\ \ldots \ m-1,\\\varepsilon =e^{\frac {2\pi i}{m}}.\end{array}}\end{matrix}}$

(24)

‎Соотвѣтствіе между этими подстановками и четыреугольниками сѣти указано на черт. 25.

Положивъ въ предыдущихъ формулахъ $m=2$, найдемъ подстановки четверичной группы.

Основныя подстановки ея суть:

$S_{\text{ч}}(u)=-u,\ {\mathfrak {T}}_{\text{ч}}(u)={\frac {1}{u}}.$

(25)

‎Онѣ обѣ 2-го порядка.

Вся совокупность четырехъ подстановокъ нормальной четверичной группы такова:

$1\,.\,u=u,\ S_{\text{ч}}(u)=-u,\ {\mathfrak {T}}_{\text{ч}}(u)={\frac {1}{u}},\ S_{\text{ч}}{\mathfrak {T}}_{\text{ч}}(u)=-{\frac {1}{u}}.$

(26)

Черт. 26‎Нормальная четверичная сѣть изображена на черт. 26.

§ 16. Группа тетраэдрическая.

Треугольникъ тетраэдрической сѣти имѣетъ углы, равные:

${\frac {\pi }{3}},\ {\frac {\pi }{3}},\ {\frac {\pi }{2}}.$^[8]

‎I. Дадимъ тетраэдру положеніе, изображенное на черт. 20: шесть срединъ реберъ его лежатъ на осяхъ координатъ.

Тетраэдрическую сѣть, соотвѣтствующую такому положенію тетраэдра назовемъ первою нормальною тетраэдрическою сѣтью.

Въ основномъ четыреугольникѣ $0acb$ сопряженныя стороны суть: $0a$ и $0b$, $ca$ и $cb$.

Черт. 27

Возьмемъ пару соотвѣтственныхъ точекъ $u$ и $u'$ на сторонахъ $0a$ и $0b$. Ясно, что:

$u=\rho e^{-{\frac {\pi i}{4}}},\ u'=-\rho e^{-{\frac {\pi i}{4}}},$

(27)

‎гдѣ $\rho$ меньше длины ${\overline {0a}}$^[9]:

$\rho <{\overline {0a}}.$

‎Изъ формулъ (27) слѣдуетъ, что:

$u'=-u.$

(28)

‎Подстановка ${\mathfrak {T}}$, преобразующая сторону $0a$ въ $0b$, такова:

${\mathfrak {T}}(u)=-u.$

(29)

‎Возьмемъ пару соотвѣтственныхъ точекъ $u$ и $u'$ на сторонахъ $ca$ и $cb$.

Не трудно видѣть, что:

$u=-1+{\sqrt {2}}e^{\psi i},\ u'=-i+{\sqrt {2}}e^{\left({\frac {\pi }{2}}-\psi \right)i},$

(30)

‎гдѣ $\psi$ перемѣнная величина.

Изъ формулъ (30) слѣдуетъ:

$(u+1)(u'+i)=2i,$

‎откуда:

$u'=i{\frac {1-u}{1+u}}.$

(31)

‎Подстановка $S$, преобразующая сторону $ca$ въ сопряженную съ нею $cb$, такова:

$S(u)=i{\frac {1-u}{1+u}}.$

(32)

‎Подстановки $S$ и ${\mathfrak {T}}$ суть основныя подстановки первой нормальной тетраэдрической группы.

Укажемъ на одну простую неосновную подстановку этой группы: вычислимъ коэффиціенты подстановки, преобразующей треугольникъ $0ac$ въ треугольникъ $\infty df$.

Соотвѣтственныя вершины этихъ треугольниковъ суть: 0 и $\infty$, $a$ и $d$, $c$ и $f$.

Подстановка, преобразующая точки $0,\ a,\ c$ соотвѣтственно въ $\infty ,\ d,\ f$, и есть искомая подстановка—этими условіями она опредѣлена вполнѣ.

Весьма простыми вычисленіями находимъ, что:

${\begin{array}{ll}a={\dfrac {{\sqrt {6}}-{\sqrt {2}}}{2}}e^{-{\frac {\pi i}{4}}},&c={\dfrac {{\sqrt {6}}-{\sqrt {2}}}{2}}e^{\frac {\pi i}{4}},\\d={\dfrac {{\sqrt {6}}+{\sqrt {2}}}{2}}e^{\frac {\pi i}{4}},&f={\dfrac {{\sqrt {6}}+{\sqrt {2}}}{2}}e^{-{\frac {\pi i}{4}}}.\end{array}}$

(33)

‎Отсюда слѣдуетъ:

$ad=1,\ cf=1.$

‎или:

$d={\frac {1}{a}},\ f={\frac {1}{c}}.$

(34)

‎Такъ какъ, кромѣ того, мы въ правѣ написать:

$\infty ={\frac {1}{0}},$

‎то мы приходимъ къ заключенію, что подстановка $U$, преобразующая треугольникъ $0ac$ въ $\infty df$, такова:

$U(u)={\frac {1}{u}},$

(35)

‎Для отличія символовъ подстановокъ тетраэдрической группы отъ символовъ иныхъ подстановокъ, мы будемъ отмѣчать ихъ индексомъ «т» (тетраэдръ).

Итакъ, мы нашли двѣ основныя подстановки первой нормальной тетраэдрической группы:

$\left.{\begin{array}{l}S_{\text{т}}(u)=i{\dfrac {1-u}{1+u}},\\{\mathfrak {T}}_{\text{т}}(u)=-u,\end{array}}\right\}$

(36)

‎и одну весьма простую неосновную подстановку:

$U_{\text{т}}(u)={\frac {1}{u}}.$

(37)

Подстановка $S_{\text{т}}$—третьяго порядка, ${\mathfrak {T}}_{\text{т}}$ и $U_{\text{т}}$—втораго порядка.

Всѣ 12 подстановокъ 1-ой нормальной тетраэдрической группы исчерпываются слѣдующими формулами:

$\left.{\begin{matrix}1\,.\,u=u,\ S_{\text{т}}(u)=i{\dfrac {1-u}{1+u}},\ S_{\text{т}}^{2}(u)={\dfrac {i-u}{i+u}},\\{\mathfrak {T}}_{\text{т}}(u)=-u,\ {\mathfrak {T}}_{\text{т}}S_{\text{т}}(u)=-i{\dfrac {1-u}{1+u}},\\{\mathfrak {T}}_{\text{т}}S_{\text{т}}^{2}(u)=-{\dfrac {i-u}{i+u}},\\U_{\text{т}}(u)={\dfrac {1}{u}},\ U_{\text{т}}S_{\text{т}}(u)=-i{\dfrac {1+u}{1-u}},\\U_{\text{т}}S_{\text{т}}^{2}(u)={\dfrac {i+u}{i-u}},\\{\mathfrak {T}}_{\text{т}}U_{\text{т}}(u)=-{\dfrac {1}{u}},\ {\mathfrak {T}}_{\text{т}}U_{\text{т}}S_{\text{т}}(u)=i{\dfrac {1+u}{1-u}},\\{\mathfrak {T}}_{\text{т}}U_{\text{т}}S_{\text{т}}^{2}(u)=-{\dfrac {i+u}{i-u}}.\end{matrix}}\right\}$

(38)

‎Соотвѣтствіе между подстановками группы и четыреугольниками сѣти указано на черт. 27.

Изъ этого чертежа, между прочимъ, видно, что

$U_{\text{т}}(u)=S_{\text{т}}^{2}{\mathfrak {T}}_{\text{т}}S_{\text{т}},$

(39)

‎въ чемъ также очень легко убѣдиться повѣркой при помощи формулъ (38).

Изъ чертежа 27 видно, что подстановка ${\mathfrak {T}}_{\text{т}}S_{\text{т}}$ есть эллиптическая подстановка, соотвѣтствующая повороту сферы на уголъ ${\frac {2\pi }{3}}$ около оси, одинъ изъ полюсовъ которой проэктируется въ точку $a$.

Слѣдовательно это подстановка 3-го порядка:

${\mathfrak {T}}_{\text{т}}S_{\text{т}}{\mathfrak {T}}_{\text{т}}S_{\text{т}}{\mathfrak {T}}_{\text{т}}S_{\text{т}}=1.$

(40)

‎Символическихъ соотношеній, подобныхъ (40), можно вывести довольно много, пользуясь чертежемъ 27, но они намъ въ дальнѣйшемъ не будутъ нужны.

Обратимъ вниманіе на то, что всѣ подстановки четверичной группы (26) входятъ въ составъ тетраэдрической группы (38):

$S_{\text{ч}}={\mathfrak {T}}_{\text{т}},\ {\mathfrak {T}}_{\text{ч}}=U_{\text{т}}.$

(41)

‎Чтобы изъ четверичной группы получить тетраэдрическую, мы должны къ подстановкамъ четверичной группы присоединить ихъ комбинаціи съ тетраэдрическими подстановками:

$S_{\text{т}},\ S_{\text{т}}^{2}.$

‎Преобразуя^[10] четверичную группу посредствомъ подстановокъ $S_{\text{т}}$ и $S_{\text{т}}^{2}$, мы снова получаемъ ту же четверичную группу. Слѣдовательно четверичная группа есть особая часть тетраэдрической.

Отношеніе порядковъ этихъ группъ (показатель сложности) равно 3.

Отсюда слѣдуетъ, что функція, инваріантная относительно подстановокъ четверичной группы, выражается раціонально черезъ функцію, инваріантную относительно подстановокъ тетраэдрической группы; а эта послѣдняя функція выражается черезъ первую при посредствѣ одного кубичнаго радикала. Эти формулы мы построимъ въ главѣ VII и онѣ дадутъ намъ возможность рѣшить въ радикалахъ тетраэдрическое уравненіе.

II. Построимъ теперь сѣть, соотвѣтствующую другому положенію тетраэдра въ сферѣ: помѣстимъ тетраэдръ въ сферѣ такъ, чтобы одна вершина его лежала въ сѣверномъ полюсѣ сферы и чтобы одно изъ реберъ его пересѣкало положительное направленіе дѣйствительной оси. Сѣть, соотвѣтствующая такому положенію тетраэдра, изображена на черт. 28.

Черт. 28Такую сѣть мы условимся называть второю нормальною тетраэдрическою сѣтью, а соотвѣтствующую ей группу — второю нормальною тетрадэрическою группою.

Примемъ $0abc$ за основной четыреугольникъ сѣти 28.

Сопряженныя стороны его суть: $0a$ и $0c$, $ba$ и $bc$.

Пользуясь тѣми же пріемами, которые мы прилагали выше, мы находимъ, что подстановка $S'_{\text{т}}$, преобразующая сторону $0a$ въ $0c$, выражается такъ:

$S'_{\text{т}}(u)=\varepsilon u,$ гдѣ $\varepsilon =e^{\frac {2\pi i}{3}};$

(42)

‎подстановка же ${\mathfrak {T}}'_{\text{т}}(u)$, преобразующая сторону $ba$ въ $bc$, такова:

${\mathfrak {T}}'_{\text{т}}(u)={\frac {{\sqrt {2}}-u}{{\sqrt {2}}u+1}}.$[11]

(43)

‎III. Возьмемъ тетраэдръ въ положеніи, соотвѣтствующемъ первой нормальной группѣ и построимъ соотвѣтствующій ему икосаэдръ: онъ изображенъ на черт. 22. Повернемъ икосаэдръ вмѣстѣ съ тетраэдромъ около мнимой оси плоскости на уголъ $\theta$, отмѣченный на чертежѣ 22. Икосаэдръ приметъ положеніе, изображенное на черт. 24, а тетраэдръ—нѣкоторое новое положеніе, нами еще не разсмотрѣнное.

Сѣть, соотвѣтствующая такому положенію тетраэдра, условимся называть третьею нормальною тетраэдрическою сѣтью.

Изъ сказаннаго слѣдуетъ, что первая нормальная тетраэдрическая сѣть преобразуется въ 3-ю посредствомъ подстановки $\sigma$, выражаемой формулами (17) и (16).

Третья нормальная тетраэдрическая группа будетъ имѣть для насъ лишь вспомогательное значеніе при сравненіи формъ икосаэдрическаго типа съ формами типа тетраэдрическаго.

Поэтому мы не будемъ теперь вычислять основныхъ подстановокъ этой группы и только обозначимъ ихъ буквами:

$S''_{\text{т}}$ и ${\mathfrak {T}}''_{\text{т}}.$

‎§ 17. Группа октаэдрическая.

Углы треугольника октаэдрической сѣти суть: ${\frac {\pi }{4}},\ {\frac {\pi }{3}},\ {\frac {\pi }{2}}.$

I. Возьмемъ октаэдръ въ положеніи, изображенномъ на черт. 21: его вершины лежатъ на осяхъ координатъ, къ которымъ отнесена сфера.

Сѣть, соотвѣтствующую такому положенію октаэдра, мы назовемъ первою нормальною октаэдрическою сѣтью. Она изображена на черт. 29.

Примемъ за основной четыреугольникъ ея $0abc$. Сопряженныя стороны его суть: $0a$ и $0c$, $ba$ и $bc$. Основныя подстановки $S_{\text{о}}$ и ${\mathfrak {T}}_{\text{о}}$, преобразующія $0a$ въ $0c$ и $ba$ въ $bc$, выражаются такъ:

$\left.{\begin{array}{l}S_{\text{о}}(u)=iu,\\{\mathfrak {T}}_{\text{о}}={\dfrac {1-u}{1+u}}.\end{array}}\right\}$[12]

(44)

Формулы (44) даютъ выраженія основныхъ подстановокъ первой нормальной октаэдрической группы.

Черт. 29

Первая изъ нихъ 4-го, а вторая—2-го порядка.

Укажемъ на одну весьма простую неосновную подстановку, преобразующую треугольникъ $0bc$ въ $\infty df$. Примѣняя совершенно такія же разсужденія, какъ и въ § 16, находимъ, что искомая подстановка выражается такъ:

$U_{\text{о}}(u)={\frac {1}{u}}.$

(45)

‎Вся совокупность 24 подстановокъ первой нормальной октаэдрической группы исчерпывается формулами:

$\left.{\begin{array}{l}\quad \quad \quad S_{\text{о}}^{k}(u)=i^{k}u,\\\quad \quad \quad S_{\text{о}}^{k}(u){\mathfrak {T}}_{\text{о}}S_{\text{о}}^{h}(u)=i^{k}{\dfrac {1-i^{h}u}{1+i^{h}u}},\\\quad \quad \quad S_{\text{о}}^{k}(u)U_{\text{о}}(u)={\dfrac {i^{k}}{u}},\\{\text{гдѣ:}}\\\quad \quad \quad k,\;h=0,\;1,\;2,\;3.\end{array}}\right\}$

(46)

‎Соотвѣтствіе между подстановками группы и четыреугольниками сѣти указано на самомъ черт. 29. Изъ черт. 29 видно, что подстановка $U_{\text{о}}$ выражается черезъ основныя подстановки $S_{\text{о}}$ и ${\mathfrak {T}}_{\text{о}}$ формулою:

$U_{\text{о}}={\mathfrak {T}}_{\text{о}}S_{\text{о}}^{2}{\mathfrak {T}}_{\text{о}},$

(47)

‎въ чемъ легко убѣдиться и непосредственною повѣркою. Изъ черт. 29, между прочимъ, видно, что подстановка $S_{\text{о}}{\mathfrak {T}}_{\text{о}}$ соотвѣтствуетъ повороту сферы на уголъ ${\frac {2\pi }{3}}$ около оси, одинъ изъ полюсовъ которой проэктируется въ точку $c$. Слѣдовательно $S_{\text{о}}{\mathfrak {T}}_{\text{о}}$ есть эллиптическая подстановка 3-го порядка:

$S_{\text{о}}{\mathfrak {T}}_{\text{о}}S_{\text{о}}{\mathfrak {T}}_{\text{о}}S_{\text{о}}{\mathfrak {T}}_{\text{о}}=1.$

(48)

‎Сравнивая октаэдрическую группу (46) съ тетраэдрической группой (38), мы замѣчаемъ, что основныя подстановки тетраэдрической группы входятъ въ октаэдрическую:

$S_{\text{т}}=S_{\text{о}}{\mathfrak {T}}_{\text{о}},\ {\mathfrak {T}}_{\text{т}}=S_{\text{о}}^{2}.$

(49)

‎Чтобы изъ тетраэдрической группы получить октаэдрическую, мы должны присоединить къ подстановкамъ тетраэдрической группы комбинаціи этихъ подстановокъ съ октаэдрической подстановкой $S_{\text{о}}$. Преобразуя тетраэдрическую группу подстановкою $S_{\text{о}}$, мы опять получаемъ ту же тетраэдрическую группу. Слѣдовательно тетраэдрическая группа есть особая часть октаэдрической. Отношеніе порядковъ этихъ группъ (показатель сложности) равно 2.

Отсюда слѣдуетъ, что всякая функція, инваріантная по отношенію къ подстановкамъ октаэдрической группы, выражается раціонально черезъ функцію, инваріантную по отношенію къ подстановкамъ группы тетраэдрической; обратно же—вторая функція выражается черезъ первую при помощи одного квадратнаго радикала. Эти формулы мы построимъ въ главѣ VII. Благодаря имъ, умѣя рѣшить въ радикалахъ тетраэдрическое уравненіе, мы будемъ въ состояніи рѣшить въ радикалахъ также и уравненіе октаэдрическое.

II. Возьмемъ тетраэдръ въ положеніи, соотвѣтствующемъ 2-ой нормальной тетраэдрической сѣти и соотвѣтствующій ему октаэдръ.

Черт. 30

Два противоположныхъ центра граней его помѣстятся въ полюсахъ сферы. Сѣть, соотвѣтствующая такому положенію октаэдра, изображена на черт. 30.

Сѣть, опредѣляемую этими условіями, мы назовемъ второю нормальною октаэдрическою сѣтью.

Примемъ за основной четыреугольникъ $0gbf$.

Сопряженныя стороны его суть: $0g$ и $0f$, $bg$ и $bf$. Подстановки $S'_{\text{о}}$ и ${\mathfrak {T}}'_{\text{о}}$^[13], преобразующія $0g$ въ $0f$ и $bg$ въ $bf$, выражаются такъ:

${\begin{matrix}\left.{\begin{array}{l}S'_{\text{о}}(u)=\varepsilon u,\\{\mathfrak {T}}'_{\text{о}}={\dfrac {1+{\sqrt {2}}\varepsilon ^{2}u}{u-{\sqrt {2}}\varepsilon }},\end{array}}\right\}&{\text{гдѣ}}&\varepsilon =e^{\frac {2\pi i}{3}}.\end{matrix}}$[14]

(50)

‎Ясно, что сѣть 30 можетъ быть получена изъ сѣти 29 тѣмъ же линейнымъ преобразованіемъ, которое сѣть 27 преобразуетъ въ сѣть 28.

III. Возьмемъ тетраэдръ въ положеніи, соотвѣтствующемъ третьей нормальной тетраэдрической сѣти и построимъ соотвѣтствующій ему октаэдръ. Сѣть, соотвѣтствующую такому положенію октаэдра, назовемъ третьею нормальною октаэдрическою сѣтью. Она получается изъ 1-ой нормальной октаэдрической сѣти преобразованіемъ посредствомъ подстановки $\sigma$, гдѣ $\sigma$ есть линейная подстановка (17), найденная въ § 14.

Основныя подстановки третьей нормальной октаэдрической группы мы будемъ обозначать такъ:

$S'_{\text{о}}$ и ${\mathfrak {T}}'_{\text{о}}.$

‎Долѣе на этой группѣ мы не останавливаемся потому, что она будетъ имѣть для насъ лишь вспомогательное значеніе.

§ 18. Группа икосаэдрическая.

I. Помѣстимъ икосаэдръ въ сферѣ такъ, какъ изображено на черт. 24. Сѣть, соотвѣтствующую такому положенію икосаэдра, назовемъ первою нормальною икосаэдрическою сѣтью.

Она изображена на чертежѣ I^[15].

За основную область икосаэдрической группы мы примемъ четыреугольникъ $0abc$. Сопряженныя стороны его суть: $0a$ и $0c$, $ba$ и $bc$.

Подстановка $S_{\text{и}}$, преобразующая сторону $0a$ въ $0c$, какъ легко видѣть, такова:

$S_{\text{и}}=\varepsilon u,$ гдѣ $\varepsilon =e^{\frac {2\pi i}{5}}.$

(51)

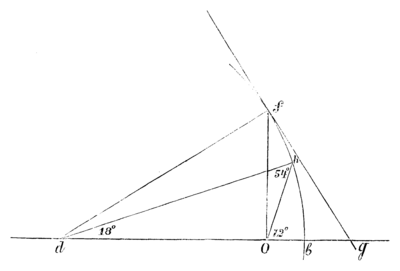
‎Подстановка ${\mathfrak {T}}_{\text{и}}$, преобразующая сторону $ba$ въ $bc$, получается тѣмъ же способомъ, но вычисленія нѣсколько сложнѣе. Разсмотримъ эти вычисленія подробно.

Черт. 31

Для ясности нѣкоторыя части чертежа I изображены въ большемъ масштабѣ на черт. 31.

Точка $f$ лежитъ на экваторѣ сферы; поэтому:

${\overline {0f}}=1.$

Изъ черт. I видно, что:

${\overline {0h}}={\overline {0g}},\;{\overline {df}}={\overline {dh}}$

‎Прямая $0f$ перпендикулярна къ $dg$.

Изъ треугольника $dh0$ (черт. 31) находимъ:

${\overline {0h}}={\overline {d0}}{\frac {sin\,18^{\circ }}{sin\,54^{\circ }}}.$

‎Изъ прямоугольнаго треугольника $dfg$ находимъ:

${\overline {f0}}^{2}={\overline {d0}}.{\overline {0g}}.$

‎Изъ сказаннаго слѣдуетъ:

$1={\overline {d0}}^{2}{\frac {sin\,18^{\circ }}{sin\,54^{\circ }}},\;{\overline {d0}}={\frac {{\sqrt {5}}+1}{2}},\;{\overline {b0}}={\frac {{\sqrt {5}}-1}{2}};$

‎далѣе:

${\overline {df}}={\sqrt {{\overline {d0}}.{\overline {dg}}}}={\sqrt {\frac {5+{\sqrt {5}}}{2}}}.$

‎Взявъ пару соотвѣтственныхъ точекъ $u$ и $u'$ на сопряженныхъ сторонахъ $ba$ и $bc$, находимъ:

$\left.{\begin{array}{l}u=-{\dfrac {{\sqrt {5}}+1}{2}}+{\sqrt {\dfrac {5+{\sqrt {5}}}{2}}}e^{-\psi i},\\u'=-{\dfrac {{\sqrt {5}}+1}{2}}+{\sqrt {\dfrac {5+{\sqrt {5}}}{2}}}e^{\psi i},\end{array}}\right\}$

(52)

‎гдѣ $\psi$ перемѣнная величина.

Отсюда:

$\left(u+{\frac {{\sqrt {5}}+1}{2}}\right)\left(u'+{\frac {{\sqrt {5}}+1}{2}}\right)={\frac {5+{\sqrt {5}}}{2}}.$

(53)

‎Такъ какъ:

$-{\frac {{\sqrt {5}}+1}{2}}=\varepsilon ^{2}+\varepsilon ^{3},$ гдѣ $\varepsilon =e^{\frac {2\pi i}{5}},$

‎то изъ уравненія (53), находимъ:

$u'={\frac {1+(\varepsilon ^{2}+\varepsilon ^{3})u}{u-(\varepsilon ^{2}+\varepsilon ^{3})}}.$

(54)

‎Искомая подстановка ${\mathfrak {T}}_{\text{и}}(u)$ выражается такъ:

${\mathfrak {T}}_{\text{и}}(u)={\frac {1+(\varepsilon ^{2}+\varepsilon ^{3})u}{u-(\varepsilon ^{2}+\varepsilon ^{3})}}.$

(55)

‎Основныя подстановки 1-ой нормальной икосаэдрической группы суть:

$\left.{\begin{array}{l}S_{\text{и}}(u)=\varepsilon u,\\{\mathfrak {T}}_{\text{и}}(u)={\dfrac {1+(\varepsilon ^{2}+\varepsilon ^{3})u}{u-(\varepsilon ^{2}+\varepsilon ^{3})}},\\{\text{гдѣ }}\varepsilon =e^{\frac {2\pi i}{5}}.\end{array}}\right\}$

(56)

‎Первая изъ нихъ 5-го, а вторая—2-го порядка.

Обратимъ вниманіе на одну очень простую неосновную подстановку $U_{\text{и}}$, преобразующую треугольникъ $0bc$ въ эквивалентный ему треугольникъ $\infty kl$. Соотвѣтственныя вершины этихъ треугольниковъ суть: 0 и $\infty$, $b$ и $k$, $c$ и $l$. Разсужденіями, подобными приведеннымъ въ § 16, находимъ, что искомая подстановка $U_{\text{и}}$ выражается такъ:

$U_{\text{и}}(u)=-{\frac {1}{u}}.$

(57)

‎Вся совокупность 60 подстановокъ первой нормальной икосаэдрической группы исчерпывается формулами:

$\left.{\begin{array}{l}S_{\text{и}}^{k}(u)=\varepsilon ^{k}u,\;S_{\text{и}}^{k}U_{\text{и}}(u)=-{\dfrac {\varepsilon ^{k}}{u}},\\S_{\text{и}}^{k}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{h}(u)=\varepsilon ^{k}{\dfrac {1+(\varepsilon ^{2}+\varepsilon ^{3})\varepsilon ^{h}u}{\varepsilon ^{h}u-(\varepsilon ^{2}+\varepsilon ^{3})}},\\S_{\text{и}}^{k}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{h}U_{\text{и}}=-{\dfrac {u-(\varepsilon ^{2}+\varepsilon ^{3})\varepsilon ^{h}}{\varepsilon ^{h}+(\varepsilon ^{2}+\varepsilon ^{3})u}},\\{\text{гдѣ }}k,\;h=0,\;1,\;2,\;3,\;4.\end{array}}\right\}$

(58)

‎Соотвѣтствія между подстановками группы и четыреугольниками икосаэдрической сѣти указаны на чертежѣ I.

Изъ чертежа I видно, что

$U=S_{\text{и}}^{2}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{3}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{2}{\mathfrak {T}}_{\text{и}}.$

(59)

‎Кромѣ того мы замѣчаемъ, что подстановка $S_{\text{и}}{\mathfrak {T}}_{\text{и}}$ соотвѣтствуетъ повороту сферы на уголъ ${\frac {2\pi }{3}}$ около оси, одинъ изъ полюсовъ которой проэктируется въ точку $c$. Слѣдовательно подстановка

$S_{\text{и}}{\mathfrak {T}}_{\text{и}}$

‎—третьяго порядка:

$S_{\text{и}}{\mathfrak {T}}_{\text{и}}S_{\text{и}}{\mathfrak {T}}_{\text{и}}S_{\text{и}}{\mathfrak {T}}_{\text{и}}=1.$

(60)

‎II. Возьмемъ икосаэдръ въ положеніи, указанномъ на черт. 22.

Сѣть, соотвѣтствующую такому положенію икосаэдра мы назовемъ второю нормальною икосаэдрическою сѣтью. Она изображена на чертежѣ II^[16]. Ясно, что эта сѣть можетъ быть получена изъ первой преобразованіемъ посредствомъ подстановки $\sigma ^{-1}$, опредѣляемой формулою (18).

Подстановки второй нормальной икосаэдрической группы мы не вычисляемъ потому, что онѣ намъ нужны не будутъ.

---

Выше мы видѣли, что положеніе икосаэдра не мѣняется отъ поворотовъ, не мѣняющихъ положенія соотвѣтствующаго ему тетраэдра. Отсюда слѣдуетъ, что въ первую нормальную икосаэдрическую группу входитъ третья нормальная тетраэдрическая группа, а во вторую нормальную икосаэдрическую группу входитъ первая нормальная тетраэдрическая группа.

Тетраэдрическая группа, входящая въ икосаэдрическую, не составляетъ собой части ея. Въ этомъ кроется существенное различіе икосаэдрической группы отъ остальныхъ разсмотрѣнныхъ нами группъ. Въ главѣ VII мы увидимъ, что вслѣдствіе сказанной особенности икосаэдрической группы, икосаэдрическое уравненіе не разрѣшимо въ радикалахъ.

§ 19. Циклическая группа конечнаго порядка.

Циклическая группа состоитъ изъ степеней одной и той же подстановки:

$S^{0},\;S^{1},\;S^{2},\;S^{3},\;\ldots$

(61)

‎Она можетъ быть конечнаго порядка только тогда, когда подстановка $S$ есть эллиптическая подстановка конечнаго порядка. Порядокъ группы (61) равенъ порядку подстановки $S$.

Возьмемъ сначала эллиптическую подстановку конечнаго порядка $m$ въ нормальной формѣ:

$S'(u)=e^{\frac {2h\pi i}{m}}u,$

(62)

‎гдѣ $k$ и $m$ числа взаимно простыя.

Взявъ наименьшій положительный корень $\alpha$ сравненія:

$h\alpha \equiv 1({\text{мод.}}m),$

(63)

‎мы найдемъ:

$S'^{\,\alpha }(u)=e^{\frac {2\pi i}{m}}u.$

(64)

‎Итакъ, въ разсматриваемую циклическую группу входитъ подстановка:

$S(u)=e^{\frac {2\pi i}{m}}u,$

(65)

‎или, короче:

$S(u)=\varepsilon u,$ гдѣ $\varepsilon =e^{\frac {2\pi i}{m}}.$

(66)

‎Группа можетъ быть представлена въ такомъ видѣ:

$S^{0}=1,\;S,\;S^{2},\ldots \;S^{m-1}.$

(67)

‎Не трудно убѣдиться въ томъ, что основная область этой группы можетъ быть представлена въ видѣ безконечной части плоскости ограниченной двумя прямыми, выходящими изъ начала координатъ и наклоненными другъ къ другу подъ угломъ ${\frac {2\pi }{m}}$.

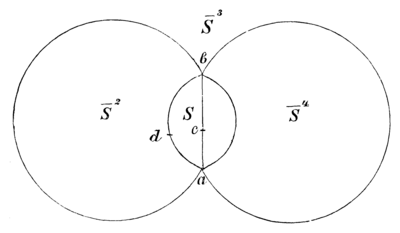
Черт. 32Покрывъ всю плоскость сѣтью такихъ областей, какъ указано на черт. 32, мы получимъ сѣть, которая соотвѣтствуетъ нормальной циклической группѣ (67) въ томъ же самомъ смыслѣ, въ какомъ разсмотрѣнныя выше сѣти четыреугольниковъ соотвѣтствовали группамъ: двупирамидной, тетраэдрической, и т. д.

Дѣйствительно, если мы возьмемъ въ какой либо изъ $m$ областей произвольную точку $u$, то въ каждой изъ остальныхъ областей найдется единственная эквивалентная ей точка относительно подстановокъ циклической группы (67).

Если мы хотимъ построить какую нибудь (не нормальную) циклическую сѣть, то должны преобразовать сѣть 32 какою нибудь линейной подстановкой. При этомъ точки $O$ и $\infty$ преобразуются въ нѣкоторыя двѣ, вообще говоря, конечныя точки $a$ и $b$, а лучи, идущіе на черт. 32 изъ точки $O$ въ безконечность, преобразуются въ дуги круговъ, соединяющія точки $a$ и $b$. Получится сѣть, изображенная на черт. 33. Основная подстановка ${\bar {S}}$ этой группы есть та подстановка, которая преобразуетъ одну изъ дугъ, напр., $acb$ въ ближайшую слѣдующую за нею: въ $adb$. Группа, соотвѣтствующая сѣти 33, представится въ такомъ видѣ:

${\bar {S}}^{0}=1,\;{\bar {S}},\;{\bar {S}}^{2},\ldots \;{\bar {S}}^{m-1}.$

(68)

Черт. 33

Основная область циклической группы имѣетъ видъ двуугольника $acbda$, какъ мы уже замѣчали выше.

Такъ какъ всякая группа содержитъ въ себѣ всѣ степени всякой подстановки, входящей въ эту группу, то циклическая группа входитъ во всякую группу.

§ 20. Конечныя группы бинарныхъ линейныхъ подстановокъ.

Бинарною подстановкою, какъ мы уже говорили въ главѣ I, мы называемъ преобразованіе двухъ перемѣнныхъ $y_{1},\ y_{2}$ такого вида:

$\left.{\begin{array}{l}{\bar {y}}_{1}=\alpha y_{1}+\beta y_{2},\\{\bar {y}}_{2}=\gamma y_{1}+\delta y_{2},\end{array}}\right\}$

(69)

‎гдѣ $\alpha ,\ \beta ,\ \gamma ,\ \delta$ какія либо постоянныя числа. Для краткости мы будемъ обозначать бинарную подстановку (69) такимъ символомъ:

${\begin{pmatrix}\alpha ,&\beta \\\gamma ,&\delta \end{pmatrix}}.$

(70)

‎Опредѣлителемъ бинарной линейной подстановки (70) называется величина:

$\alpha \delta -\beta \gamma .$

‎Перемноживъ символически двѣ линейныя бинарныя подстановки, мы получаемъ опять линейную бинарную подстановку, опредѣлитель которой равенъ произведенію опредѣлителей перемноженныхъ подстановокъ.

Если нѣкоторая совокупность линейныхъ бинарныхъ подстановокъ образуетъ группу^[17], то мы назовемъ ее группою бинарныхъ подстановокъ.

Каждой бинарной линейной подстановкѣ (70) соотвѣтствуетъ единственная неоднородная линейная подстановка:

${\bar {u}}={\frac {\alpha u+\beta }{\gamma u+\delta }},$

(71)

‎но не обратно: каждой неоднородной подстановкѣ (71) соотвѣтствуетъ безконечное множество бинарныхъ подстановокъ, которыя можно изобразить символомъ:

${\begin{pmatrix}\rho \alpha ,&\rho \beta \\\rho \gamma ,&\rho \delta \end{pmatrix}},$

(72)

‎гдѣ $\rho$ произвольное постоянное.

Если двѣ группы одинаковаго порядка составлены изъ одинаковаго числа основныхъ подстановокъ такъ, что каждой подстановкѣ одной группы соотвѣтствуетъ единственная подстановка другой и обратно, то мы назовемъ ихъ изоморфными группами^[18].

Возьмемъ группу $\Gamma$ бинарныхъ линейныхъ подстановокъ, найдемъ соотвѣтствующія имъ неоднородныя линейныя подстановки. Эти послѣднія, конечно, образуютъ нѣкоторую группу $G$ неоднородныхъ линейныхъ подстановокъ.

Если порядокъ группы $\Gamma$ конечный, то и порядокъ группы $G$ будетъ конечный. Эта группа будетъ принадлежать къ одному изъ типовъ: циклическому, двупирамидному, тетраэдрическому, октаэдрическому или икосаэдрическому.

Посмотримъ, могутъ ли быть группы $\Gamma$ и $G$ изоморфны между собою.

Для простоты мы можемъ предполагать группу $G$ приведенною къ нормальному виду^[19].

I. Пусть $G$ группа циклическая и пусть она изоморфна соотвѣтствующей ей группѣ $\Gamma$.

Группа $G$ составлена изъ одной основной подстановки:

$S(u)=\varepsilon u,$ гдѣ $\varepsilon =e^{\frac {2\pi i}{m}}.$

(66)

‎Соотвѣтствующая ей основная бинарная подстановка группы $\Gamma$ такова:

${\begin{pmatrix}\rho \varepsilon ,&0\\0,&\rho \end{pmatrix}},$

(73)

‎гдѣ $\rho$—нѣкоторый постоянный множитель.

Такъ какъ

$S^{m}=1,$

(74)

‎то должно имѣть мѣсто символическое равенство:

$\sigma ^{m}=1,$

(75)

‎или:

${\begin{pmatrix}\rho ^{m}\varepsilon ^{m},&0\\0,&\rho ^{m}\end{pmatrix}},$

(76)

‎откуда:

$\rho ^{m}=1.$

(77)

‎Если $\rho$ есть корень $m$-ой степени изъ 1, то циклическая группа бинарныхъ линейныхъ подстановокъ:

$\sigma ^{0}=1,\;\sigma ,\;\sigma ^{2},\ldots \;\sigma ^{m-1}$

(78)

‎изоморфна группѣ неоднородныхъ линейныхъ подстановокъ:

$S^{0}=1,\;S,\;S^{2},\ldots \;S^{m-1}.$

(67)

‎II. Пусть группа $G$ двупирамидная и изоморфна соотвѣтствующей ей группѣ $\Gamma$.

Основныя подстановки двупирамидной группы суть:

$\left.{\begin{array}{l}S_{\text{д}}(u)=\varepsilon u,\ {\text{гдѣ}}\ \varepsilon =e^{\frac {2\pi i}{m}},\\{\mathfrak {T}}_{\text{д}}(u)={\dfrac {1}{u}}.\end{array}}\right\}$

(23)

‎Основныя подстановки группы $\Gamma$ суть:

$\sigma ={\begin{pmatrix}\rho \varepsilon ,&0\\0,&\rho \end{pmatrix}},\;\tau ={\begin{pmatrix}0,&\rho '\\\rho ',&0\end{pmatrix}}.$

(79)

‎Такъ какъ:

$S^{m}=1,\;{\mathfrak {T}}^{2}=1,$

(80)

‎то должны имѣть мѣсто символическія равенства:

$\sigma ^{m}=1,\;\tau ^{2}=1,$

(81)

‎или:

${\begin{pmatrix}\rho ^{m}\varepsilon ^{m},&0\\0,&\rho ^{m}\end{pmatrix}}=1,\;{\begin{pmatrix}0,&\rho '^{\,2}\\\rho '^{\,2},&0\end{pmatrix}}=1,$

(82)

‎откуда:

$\rho ^{m}=1,\;\rho '^{\,2}=1.$

(83)

‎Въ группу $G$ входитъ подстановка 2-го порядка $S{\mathfrak {T}}$:

$S{\mathfrak {T}}(u)={\frac {\varepsilon }{u}}.$

(84)

‎Соотвѣтствующая ей подстановка $\sigma \tau$ тоже должна быть втораго порядка:

$(\sigma \tau )^{2}={\begin{pmatrix}0,&\rho \rho '\varepsilon \\\rho \rho ',&0\end{pmatrix}}^{2}={\begin{pmatrix}\rho ^{2}\rho '^{\,2}\varepsilon ,&0\\0,&\rho ^{2}\rho '^{\,2}\varepsilon \end{pmatrix}}=1,$

(85)

‎откуда:

$\rho ^{2}\rho '^{\,2}\varepsilon =1.$

(86)

‎Изъ равенствъ (83) и (86) слѣдуетъ:

$\rho ^{2}=e^{-{\frac {2\pi i}{m}}},$

(87)

‎откуда:

$\rho =\pm e^{-{\frac {\pi i}{m}}},$

(88)

‎и далѣе:

$\rho ^{m}=-(\pm 1)^{m}.$

(88)

‎Ясно, что послѣднее равенство не противорѣчитъ первому изъ равенствъ (83) только въ томъ случаѣ, если $m$ нечетно и если, кромѣ того, въ формулѣ (88) взятъ нижній знакъ. Въ такомъ случаѣ имѣемъ:

$\rho =-e^{-{\frac {\pi i}{m}}}.$

(90)

‎Итакъ, двупирамидная группа бинарныхъ линейныхъ подстановокъ только въ томъ случаѣ можетъ быть изоморфна соотвѣтствующей ей группѣ неоднородныхъ линейныхъ подстановокъ, если порядокъ этой группы есть число вида:

$2m=2(2p+1).$

III. Пусть группа $G$ тетраэдрическая, октаэдрическая или икосаэдрическая.

Мы уже видѣли выше, что въ составъ каждой изъ этихъ группъ входитъ группа четверичная, то есть двупирамидная, порядка

$2m=2.2.$

‎Эта четверичная группа на основаніи только что полученнаго результата не можетъ быть изоморфна соотвѣтствующей ей группѣ бинарныхъ линейныхъ подстановокъ.

Если такъ, то и вся группа $G$ не можетъ быть изоморфна группѣ $\Gamma$.

Этотъ послѣдній результатъ можно формулировать въ видѣ такой теоремы:

Теорема 4. Группы бинарныхъ подстановокъ тетраэдрическаго, октаэдрическаго и икосаэдрическаго типовъ не могутъ быть изоморфны группамъ соотвѣтствующихъ имъ неоднородныхъ линейныхъ подстановокъ.

Теорема эта принадлежитъ Клейну^[20] и имѣетъ важное значеніе для изучаемыхъ нами уравненій.

Пользуясь теоремой 4, мы можемъ нѣсколько пополнить результаты главы I.

Мы знаемъ изъ теоремы 8 главы I, что существуетъ группа бинарныхъ линейныхъ подстановокъ съ опредѣлителемъ равнымъ 1, связывающая между собою корни уравненія (20) главы I.

Порядокъ этой группы равенъ степени $n$ уравненія (20) главы I. Подстановки этой группы выражаютъ каждый корень уравненія (20) черезъ два корня того же уравненія.

Далѣе, изъ теоремы 22 главы I мы знаемъ, что отношенія корней уравненія (20) служатъ корнями уравненія (95) степени $N$, при чемъ $N$ равно $n$ или ${\frac {n}{2}}$. Уравненіе (95) главы I имѣетъ группу неоднородныхъ линейныхъ подстановокъ, соотвѣтствующую группѣ бинарныхъ линейныхъ подстановокъ уравненія (20).

Ясно, что степень $N$ уравненія (95) можетъ равняться степени $n$ уравненія (20) только въ томъ случаѣ, когда двѣ названныя группы изоморфны, а это возможно только для двупирамидной группы, степень которой есть число вида:

$2m=2(2p+1).$

‎Итакъ, для типовъ: тетраэдрическаго, октаэдрическаго и икосаэдрическаго степень $n$ уравненія (20) вдвое выше степени $N$ уравненія (95):

$n=2N.$

‎Отсюда слѣдуетъ, что въ формулахъ (106) и (107) главы I радикалъ не можетъ быть извлеченъ точно изъ подкоренныхъ выраженій; корни уравненія (20) попарно разнятся знаками.

Посмотримъ, каковы группы уравненій (20) главы I для каждаго изъ 4 типовъ.

Это суть группы бинарныхъ подстановокъ съ опредѣлителемъ 1, соотвѣтствующія группамъ неоднородныхъ линейныхъ подстановокъ, найденнымъ въ настоящей главѣ.

Имѣя неоднородную подстановку

${\bar {u}}={\frac {\alpha u+\beta }{\gamma u+\delta }},$

‎легко найти соотвѣтствующія ей бинарныя подстановки съ опредѣлителемъ 1. Это суть подстановки вида:

${\begin{pmatrix}\rho \alpha ,&\rho \beta \\\rho \gamma ,&\rho \delta \end{pmatrix}},$

‎гдѣ $\rho$ есть величина, опредѣляемая условіемъ:

$\rho ^{2}(\alpha \delta -\beta \gamma )=1.$

‎Ясно, что $\rho$ имѣетъ два значенія, разнящихся знаками.

Выполнимъ эти вычисленія для первыхъ нормальныхъ группъ, найденныхъ въ настоящей главѣ.

Въ результатѣ мы найдемъ такія выраженія основныхъ подстановокъ конечныхъ группъ бинарныхъ линейныхъ подстановокъ:

Группа двупирамидная.

$\sigma ={\begin{pmatrix}e^{\frac {\pi i}{m}},&0\\0,&e^{-{\frac {\pi i}{m}}}\end{pmatrix}},\;\tau ={\begin{pmatrix}0,&i\\i,&0\end{pmatrix}}.$

(91)

Группа тетраэдрическая.

$\sigma ={\begin{pmatrix}{\dfrac {e^{-{\frac {\pi i}{4}}}}{\sqrt {2}}},&{\dfrac {e^{\frac {3\pi i}{4}}}{\sqrt {2}}}\\{\dfrac {e^{\frac {\pi i}{4}}}{\sqrt {2}}},&{\dfrac {e^{\frac {\pi i}{4}}}{\sqrt {2}}}\end{pmatrix}},\;\tau ={\begin{pmatrix}i,&0\\0,&-i\end{pmatrix}}.$

(92)

Группа октаэдрическая.

$\sigma ={\begin{pmatrix}e^{\frac {\pi i}{4}},&0\\0,&e^{-{\frac {\pi i}{4}}}\end{pmatrix}},\;\tau ={\begin{pmatrix}-{\dfrac {i}{\sqrt {2}}},&{\dfrac {i}{\sqrt {2}}}\\{\dfrac {i}{\sqrt {2}}},&{\dfrac {i}{\sqrt {2}}}\end{pmatrix}}.$

(93)

Группа икосаэдрическая.

$\sigma ={\begin{pmatrix}-\varepsilon ^{3},&0\\0,&-\varepsilon ^{2}\end{pmatrix}},\;\tau ={\begin{pmatrix}-{\dfrac {\varepsilon -\varepsilon ^{4}}{\sqrt {5}}},&{\dfrac {\varepsilon ^{2}-\varepsilon ^{3}}{\sqrt {5}}}\\{\dfrac {\varepsilon ^{2}-\varepsilon ^{3}}{\sqrt {5}}},&{\dfrac {\varepsilon -\varepsilon ^{4}}{\sqrt {5}}}\end{pmatrix}},$ гдѣ $\varepsilon =e^{\frac {2\pi i}{5}}.$

(94)

‎Не трудно усмотрѣть, что во всѣ четыре группы входитъ подстановка:

${\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

(95)

‎т. е.

$\left.{\begin{array}{l}{\bar {y}}_{1}=-y_{1},\\{\bar {y}}_{2}=-y_{2}.\end{array}}\right\}$

‎Въ самомъ дѣлѣ:

‎для двупирамидной группы (91): $\sigma ^{m}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

‎для тетраэдрической группы (92): $\tau ^{2}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

‎для октаэдрической группы (93): $\sigma ^{4}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

‎для икосаэдрической группы (94): $\sigma ^{5}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}}.$

Слѣдовательно, порядокъ всѣхъ пяти группъ дѣйствительно вдвое выше порядка соотвѣтствующихъ имъ группъ неоднородныхъ линейныхъ подстановокъ.

Сноски

1. Случай $\lambda =\lambda _{1}=\lambda _{2}=3$ взятъ лишь для упрощенія чертежа. Разсужденія, приведенныя въ текстѣ, относятся ко всякой сѣти четыреугольниковъ.
2. Срав. Poincaré. Théorie des groupes fuchsiennes. Acta Mathem. Том I.
3. Въ этомъ мы убѣждаемся совершенно такими же разсужденіями, которыя приведены выше.
4. Основными подстановками называются такія подстановки, изъ которыхъ можно составить любую подстановку группы и которыя въ то же время независимы между собою.
5. Подробности о циклическихъ группахъ можно найти у Клейна: Vorlesungen über die Theorie der elliptischen Modulfunctionen. Стр. 186.
6. См. глава III, таблица (73).
7. По техническим причинам индексы отображаются прямым шрифтом. — Примѣчаніе редактора Викитеки.
8. См. глава III, таблица (73).
9. Мы обозначаемъ разстояніе между точками 0 и $a$ черезъ ${\overline {0a}}$.
10. Если $S_{0},\ S_{1},\ \ldots \ S_{N-1}$ суть подстановки группы и $\sigma$ есть какая-нибудь подстановка, то мы назовемъ группу: $\sigma S_{0}\sigma ^{-1},\ \sigma S_{1}\sigma ^{-1},\ \ldots \ \sigma S_{N-1}\sigma ^{-1}$
    преобразованною изъ первой посредствомъ подстановки $\sigma$. Опредѣленія и свойства понятій: особая часть группы, уравненіе, имѣющее своею группою особую часть группы даннаго уравненія, и пр. излагаются въ курсахъ высшей алгебры. См., напр., Serret. Cours d’algèbre supérieure; или: Селивановъ. Теорія алгебраическаго рѣшенія уравненій.
11. При вычисленіи этой подстановки необходимо знать величину отрѣзка ${\overline {0d}}$. Совершенно элементарнымъ путемъ мы находимъ, что ${\overline {0d}}={\frac {1}{\sqrt {2}}}.$

12. Подстановки эти вычисляются тѣми же пріемами, какъ и въ разсмотрѣнныхъ выше случаяхъ. Вычисленія никакихъ затрудненій не представляютъ.
13. При вычисленіи подстановки ${\mathfrak {T}}'_{\text{о}}$ необходимо замѣтить, что точка $d$ на чертежѣ 30 занимаетъ то же положеніе, какъ и точка $d$ на чертежѣ 28: ${\overline {0d}}={\frac {1}{\sqrt {2}}}.$

14. Не лишено интереса замѣчаніе, что тетраэдрическая подстановка ${\mathfrak {T}}'_{\text{т}}$ есть квадратъ октаэдрической ${\mathfrak {T}}'_{\text{о}}$: ${\mathfrak {T}}'_{\text{т}}={\mathfrak {T}}_{\text{о}}^{'\,2}.$

15. Въ концѣ сочиненія.
16. Въ концѣ сочиненія.
17. Выше, въ § 1, мы опредѣлили понятіе о группѣ какихъ бы то ни было операцій.
18. Holoedrisch isomorph по терминологіи нѣмецкихъ математиковъ.
19. Всякую группу $G$ неоднородныхъ линейныхъ подстановокъ можно преобразовать въ нормальную группу того же типа.
    ‎Въ самомъ дѣлѣ, построимъ сѣть, соотвѣтствующую группѣ $G$ и нормальную сѣть того же типа. Эти сѣти, какъ мы знаемъ, эквивалентны между собою. Пусть подстановка, преобразующая первую сѣть во вторую, есть $\Sigma$. Преобразуя группу $G$ подстановкою $\Sigma$, мы получаемъ нормальную группу, соотвѣтствующую взятой нами нормальной сѣти.
20. Vorlesungen über das Ikosaeder. Стр. 46.