Алгебраические уравнения, разрешимые в гипергеометрических функциях (Лахтин)/Глава IV

Алгебраические уравнения, разрешимые в гипергеометрических функциях — Глава IV. Конечные группы линейных подстановок
автор Л. К. Лахтин

§ 13. Общие приемы вычисления подстановок группы, соответствующей данной сети треугольников  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

730

§ 14. Геометрические представления для групп конечных порядков  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

736

§ 15. Группа двупирамидная  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

743

§ 16. Группа тетраэдрическая  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

746

§ 17. Группа октаэдрическая  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

753

§ 18. Группа икосаэдрическая  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

758

§ 19. Циклическая группа конечного порядка  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

762

§ 20. Конечные группы бинарных линейных подстановок  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

764

---

Глава IV.

Конечные группы линейных подстановок.

§ 13. Общие приемы вычисления подстановок группы, соответствующей данной сети треугольников.

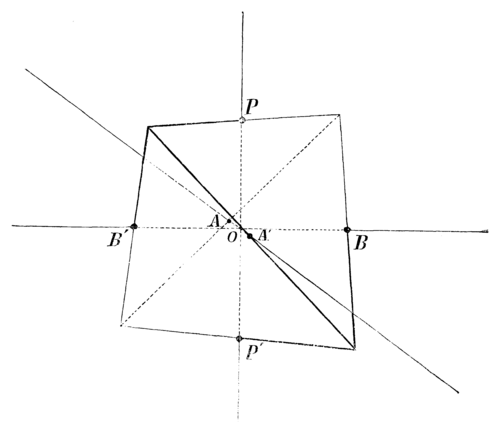
Пусть дана сеть треугольников. Соединив треугольники попарно, мы получим сеть четырехугольников. Каждый из этих четырехугольников есть основная область некоторой неизвестной нам группы линейных подстановок. Все четырехугольники эквивалентны между собой относительно подстановок этой группы.

Для краткости мы будем обозначать четырехугольники сети номерами: $1,\ 2,\ 3,\ \ldots$

Черт. 18^[1]Возьмем в четырехугольнике 1-м произвольную точку $u_{1}$ (черт. 18), строим ряд зеркальных изображений точки $u_{1}$:

$u'_{1},\ u_{1},\ u'_{2},\ u'_{3},\ \ldots$

‎В каждом четырехугольнике найдется по одной точке, соответствующей точке $u_{1}$:

$u_{1},\ u_{2},\ u_{3},\ \ldots$

‎Точки $u'_{1},\ u'_{2},\ u'_{3},\ \ldots$ будут симметричны с точками $u_{1},\ u_{2},\ u_{3},\ \ldots$ относительно диагоналей четырехугольников.

Теорема 1. Стороны четырехугольника сети попарно эквивалентны.

Будем двигать точку $u_{1}$ внутри четырехугольника 1, приближая ее к какой-нибудь точке $e$ стороны $ad$. Зеркальное изображение $u'_{1}$ будет приближаться к точке $e'$, симметричной с точкой $e$ относительно диагонали $bd$. Точка $u_{2}$, симметричная с $u'_{1}$ относительно стороны $cd$, будет приближаться к той же точке $e'$ стороны $cd$. В тот момент, когда $u_{1}$ придет в $e$, точка $u_{2}$ придет в $e'$.

Точки $u_{1}$ и $u_{2}$ суть точки соответственные в четырехугольниках 1 и 2. Они связаны между собой линейной подстановкой $S$, преобразующей четырехугольник 1 в четырехугольник 2:

$u_{2}=S(u_{1}).$

(1)

‎Если так, то:

$e'=S(e).$

(2)

‎Это последнее равенство справедливо, где бы на стороне $ad$ мы ни взяли точку $e$: сторона $ad$ эквивалентна стороне $cd$, и подстановка, преобразующая $ad$ в $cd$, есть та подстановка $S$, которая преобразует четырехугольник 1 в 2.

Будем двигать точку $u_{1}$, приближая ее к какой-нибудь точке $f$ стороны $ab$. Зеркальное изображение $u'_{1}$ будет приближаться к точке $f'$, симметричной с $f$ относительно диагонали $bd$. Точка $u_{4}$, симметричная с $u'_{1}$ относительно стороны $bc$, будет приближаться к той же точке $f'$ стороны $bc$. В тот момент, когда точка $u_{1}$ придет в $f$, точка $u_{4}$ придет в $f'$. Точки $u_{1}$ и $u_{4}$ суть соответственные точки в четырехугольниках 1 и 4; они связаны между собой линейной подстановкой ${\mathfrak {T}}$, преобразующей четырехугольник 1 в 4:

$u_{4}={\mathfrak {T}}(u_{1}).$

(3)

‎Если так, то:

$f'={\mathfrak {T}}(f).$

(4)

‎Это равенство справедливо, где бы на стороне $ab$ мы ни взяли точку $f$: сторона $cb$ эквивалентна стороне $ab$, и подстановка, преобразующая $ab$ в $cb$, есть та подстановка ${\mathfrak {T}}$, которая преобразует четырехугольник 1 в 4.

Четырехугольник 1 был взят совершенно произвольно; поэтому мы вправе сказать, что стороны всякого четырехугольника сети попарно эквивалентны^[2].

Теорема доказана.

Следуя Пуанкаре, будем называть эквивалентные стороны четырехугольника сопряженными.

Для последующего важно обратить внимание на следующее обстоятельство.

Подстановка $S^{-1}$, преобразующая сторону $cd$ в сопряженную с ней $ad$, есть та подстановка, которая преобразует четырехугольник 1 в 3^[3]; следовательно подстановка, преобразующая четырехугольник 1 в 2, обратна той, которая преобразует четырехугольник 1 в 3.

На том же основании подстановка, преобразующая четырехугольник 1 в 4, обратна той, которая преобразует четырехугольник 1 в 5.

Эти последние заключения мы можем формулировать в виде теоремы:

Теорема 2. Подстановки, преобразующие четырехугольник 1 в смежные, суть:

$S,\ {\mathfrak {T}},\ S^{-1},\ {\mathfrak {T}}^{-1}.$

(5)

‎Теорема 3. Подстановки:

$S$ и ${\mathfrak {T}}$

‎суть основные^[4] подстановки группы.

Возьмем четырехугольник 1-ый и какой-нибудь четырехугольник $m$-ый данной сети и в них отметим соответственные точки $u_{1}$ и $u_{m}$. Пусть четырехугольник $m$-ый получается из четырехугольника 1-го линейным преобразованием $\Sigma$:

$u_{m}=\Sigma (u_{1}).$

(6)

‎Будем точку $u_{m}$ перемещать так, чтобы она вышла из четырехугольника $m$-го, вступила в смежный с ним четырехугольник $m+1$-ый и пришла в совпадение с точкой $u_{m+1}$ этого последнего четырехугольника, причем под $u_{m+1}$ мы подразумеваем точку четырехугольника $m+1$-го, эквивалентную $u_{1}$ относительно подстановок группы. В то же время точка $u_{1}$ будет, необходимо, также перемещаться, выйдет из четырехугольника 1-го и вступит в один из смежных с ним четырехугольников. Для определенности положим, что она вступила в четырехугольник 2-ой.

В тот момент, когда точка $u_{m}$ пришла в $u_{m+1}$, точка $u_{1}$ достигнет $u_{2}$.

Ясно, что точки $u_{m+1}$ и $u_{2}$ связаны между собой подстановкой $\Sigma$:

$u_{m+1}=\Sigma (u_{2}).$

(7)

‎Подставив в это равенство вместо $u_{2}$ ее выражение:

$u_{2}=S(u_{1}),$

(1)

‎находим:

$u_{m+1}=\Sigma S(u_{1}).$

(8)

‎Это значит, что четырехугольник $m+1$-ый, смежный с четырехугольником $m$-м, получается из четырехугольника 1-го подстановкой:

$\Sigma S.$

(9)

‎На основании тех же рассуждений мы вправе сказать, что остальные три четырехугольника, смежные с $m$-м, получаются из четырехугольника 1-го подстановками:

$\Sigma {\mathfrak {T}},\ \Sigma S^{-1},\ \Sigma {\mathfrak {T}}^{-1}.$

(10)

‎Итак, если четырехугольник $m$-ый получается из начального четырехугольника 1-го подстановкой $\Sigma$, то четырехугольники, смежные с $m$-м, получаются из 1-го подстановками:

$\Sigma S,\ \Sigma S^{-1},\ \Sigma {\mathfrak {T}},\ \Sigma {\mathfrak {T}}^{-1}.$

(11)

‎Пользуясь этим результатом, мы можем найти подстановку, преобразующую четырехугольник 1-ый в любой четырехугольник сети. В самом деле, в теореме 2 мы видели, что четырехугольники, смежные с 1-м, получаются из него подстановками:

$S,\ {\mathfrak {T}},\ S^{-1},\ {\mathfrak {T}}^{-1}.$

(5)

‎Отсюда следует, что четырехугольники, смежные с только что перечисленными, получаются из четырехугольника 1-го подстановками:

$\left.{\begin{array}{l}S^{2},\ S{\mathfrak {T}},\ S{\mathfrak {T}}^{-1},\\{\mathfrak {T}}S,\ {\mathfrak {T}}^{2},\ {\mathfrak {T}}S^{-1},\\S^{-1}{\mathfrak {T}},\ S^{-2},\ S^{-1}{\mathfrak {T}}^{-1},\\{\mathfrak {T}}^{-1}S,\ {\mathfrak {T}}^{-1}S^{-1},\ {\mathfrak {T}}^{-2}.\end{array}}\right\}.$

(12)

‎Имея подстановки (5) и (12), мы найдем подстановки, соответствующие следующим четырехугольникам, смежным с рассмотренными, и т. д. Так, мы найдем подстановки, соответствующие всем четырехугольникам сети. Все эти подстановки будут представляться формулами вида:

$S^{\alpha }\ {\mathfrak {T}}^{\beta }\ S^{\gamma }\ {\mathfrak {T}}^{\delta }\ \ldots \ S^{\varkappa }\ {\mathfrak {T}}^{\lambda },$

(13)

‎где $\alpha ,\ \beta ,\ \gamma ,\ \delta ,\ \ldots ,\ \varkappa ,\ \lambda$ суть числа целые положительные или отрицательные. Некоторые из них могут равняться нулю.

Итак, мы доказали, что всякая подстановка группы может быть составлена из подстановок $S$ и ${\mathfrak {T}}$. Остается доказать, что эти подстановки $S$ и ${\mathfrak {T}}$ независимы между собой.

Допустим, что подстановки $S$ и ${\mathfrak {T}}$ не независимы. В таком случае одна из них должна быть степенью другой. Пусть:

${\mathfrak {T}}=S^{\alpha }.$

(14)

‎Подстановка $S$, как мы видели, преобразует сторону $da$ четырехугольника 1 в сопряженную с ней сторону $dc$; при этом точка $d$ преобразуется сама в себя.

Следовательно, точка $d$ есть одна из двух точек, не изменяемых подстановкой $S$. Если точка $d$ не меняется подстановкой $S$, то она не может меняться и подстановкой:

${\mathfrak {T}}=S^{\alpha }.$

(14)

‎Между тем мы знаем, что подстановка ${\mathfrak {T}}$ преобразует четырехугольник 1 в четырехугольник 4, не прилегающий ни к стороне $ad$, ни к стороне $dc$. Следовательно, точка $d$ подстановкой ${\mathfrak {T}}$ непременно меняется.

Такое противоречие произошло от сделанного нами допущения, что подстановки ${\mathfrak {T}}$ и $S$ не независимы между собой.

Итак, действительно, подстановки $S$ и ${\mathfrak {T}}$ суть основные подстановки группы.

Если бы, как мы допустили выше, подстановка ${\mathfrak {T}}$ была зависима от $S$, то группа была бы циклическая:

$S^{0}=1,\ S,\ S^{2},\ S^{3},\ \ldots$

(15)

‎Основной областью такой группы не служит четырехугольник. О циклической группе конечного порядка мы будем говорить в § 19 и увидим, что основной областью ее служит двуугольник, образованный дугами кругов^[5].

Посмотрим теперь, как по данной сети четырехугольников построить соответствующую ей группу линейных подстановок.

Примем один из четырехугольников сети за основной четырехугольник. Диагональной дугой окружности он делится на два треугольника, из которых один белый, а другой — черный. Стороны четырехугольника, симметричные относительно этой диагонали, суть сопряженные. Найдем линейные подстановки $S$ и ${\mathfrak {T}}$, преобразующие две стороны четырехугольника в две другие стороны, сопряженные с ними.

Эти подстановки $S$ и ${\mathfrak {T}}$ суть основные подстановки группы.

Имея основные подстановки, мы можем указанным выше способом найти подстановку, соответствующую каждому четырехугольнику сети. При этом особенности данной сети могут значительно облегчить вычисления.

Так, например, вычисления значительно упростятся, если нам удастся найти эллиптическую подстановку и известен угол соответствующего ей поворота сферы.

Во всех случаях, с которыми нам придется встретиться, все подстановки будут эллиптические и вычисления совершаются очень легко. Поэтому мы не будем останавливаться на этих вычислениях и только на чертежах будем отмечать подстановки, соответствующие каждому четырехугольнику.

§ 14. Геометрические представления для групп конечных порядков.

Вообразим вписанный в сферу один из многогранников, указанных в § 12, соответствующую ему сеть на сфере и ее стереографическую проекцию на плоскость.

Так как все подстановки группы, соответствующей этой сети, — конечного порядка, то все они эллиптические. Они соответствуют таким поворотам сферы около центра, которые приводят сеть на сфере и вписанный многогранник в их прежнее положение. Ясно, что эти повороты могут происходить около осей, проходящих или 1) через вершину многогранника, или 2) через центр его грани, или 3) через середину ребра. В первом случае поворот совершается на угол ${\frac {2\pi }{\lambda }}$, где $\lambda$ число граней многогранника, сходящихся около вершины, во втором случае поворот совершается на угол ${\frac {2\pi }{3}}$, в третьем случае — на угол $\pi$. Порядок подстановки, соответствующей повороту, равен в первом случае $\lambda$, во втором — числу 3, в третьем — числу 2.

Будем называть для краткости проекции на поверхность сферы центров граней и середин ребер многогранника — центрами граней, серединами ребер.

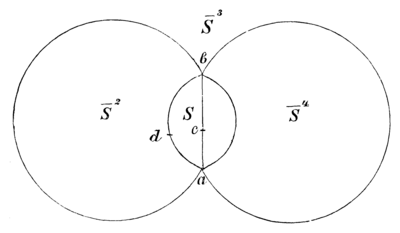
Черт. 19Из числа групп двупирамидного типа нам больше всего придется иметь дело с группой 4-го порядка, так называемой четверичной группой (Vierergruppe по Клейну). Многогранник, соответствующий четверичной группе, есть четырехгранная двупирамида. Ясно, что мы называем ее многогранником лишь ради аналогии: она имеет вид четырехугольника $APA'P'$, вписанного в сферу (черт. 19). Точки $P$ и $P'$ мы рассматриваем, как вершины четырехгранной двупирамиды, $A$ и $A'$ как вершины основания ее, а точки $B$ и $B'$, лежащие на перпендикуляре $BB'$ к плоскости $APA'P'$ — как середины ребер основания четырехгранной двупирамиды.

Ниже, на черт. 26, изображена четверичная сеть, соответствующая четырехгранной двупирамиде, изображенной на черт. 19.

Сравним между собой расположения вершин, центров граней и середин ребер для четырех видов многогранников: четырехгранной двупирамиды, тетраэдра, октаэдра и икосаэдра.

Поместим тетраэдр в сфере так, чтобы середины ребер его находились на осях координат, к которым отнесена сфера. Такое положение его изображено на черт. 20.

Ясно, что середины ребер его: $A',\ P,\ A,\ P'$ могут быть приняты за вершины четырехгранной двупирамиды; шесть середин граней тетраэдра распадаются на три группы точек, из которых каждая группа может быть принята за вершины четырехгранной двупирамиды. Это мы выразим словами:

Черт. 20

‎тетраэдру соответствует три четырехгранных двупирамиды. Обратно: четырехгранной двупирамиде соответствует один определенный тетраэдр.

Каждый поворот, соответствующий подстановке четверичной группы, приводит как четырехгранную двупирамиду, так и тетраэдр в прежнее их положение, но не обратно: некоторые повороты тетраэдрической группы будут сменять между собой три четырехгранные двупирамиды, соответствующие тетраэдру.

Отсюда заключаем, что в тетраэдрической группе заключаются три четверичные группы.

Поместим октаэдр в сфере так, чтобы вершины его лежали на осях координат. Такое положение его изображено на черт. 21.

Черт. 21

Мы видим, что вершины его совпадают с серединами ребер тетраэдра, изображенного на черт. 20.

Из числа восьми центров граней октаэдра четыре совпадают с вершинами, а остальные четыре — с центрами граней тетраэдра.

Октаэдру соответствуют два взаимно дополнительных тетраэдра, из которых один переходит в другой при повороте на угол ${\frac {\pi }{2}}$ около каждой из трех осей, соединяющих противоположные вершины октаэдра. Обратно, тетраэдру соответствует вполне определенный октаэдр.

Отсюда следует, что повороты, соответствующие подстановкам тетраэдрической группы, не меняют положения октаэдра, но не обратно: некоторые повороты октаэдрической группы сменяют между собой два тетраэдра, соответствующих октаэдру.

Отсюда заключаем, что в октаэдрическую группу входят две тетраэдрические.

Поместим, наконец, икосаэдр в сфере так, чтобы шесть середин ребер его лежали на осях координат. Такое положение его изображено на черт. 22.

Черт. 22

Середины ребер икосаэдра, лежащие на осях координат, могут быть приняты за вершины октаэдра. Все 30 середин ребер икосаэдра распадаются на 5 групп по 6 точек в каждой, причем 6 точек каждой такой группы могут служить вершинами октаэдра.

Следовательно, икосаэдру соответствует 5 октаэдров. Однако необходимо заметить, что каждому октаэдру соответствует 2 икосаэдра: повернув октаэдр на угол ${\frac {\pi }{2}}$ около какой-либо оси, соединяющей две его противоположные вершины, мы изменим положение соответствующего ему икосаэдра: переведем его из положения, изображенного на черт. 22, в положение, изображенное на черт. 23.

Черт. 23

Следовательно октаэдрическая группа не входит в состав икосаэдрической.

Возьмем снова икосаэдр, изображенный на чертеже 22. Середины ребер его, лежащие на осях координат, могут быть приняты за середины ребер тетраэдра. Так как каждому октаэдру соответствует два взаимно дополнительных тетраэдра, то икосаэдру соответствует 5 пар взаимно дополнительных тетраэдров. Каждый поворот, не меняющий положение одного из этих тетраэдров, не изменит ни положения дополнительного ему тетраэдра, ни положения икосаэдра. Каждому тетраэдру соответствует один определенный икосаэдр.

Из сказанного следует, что в икосаэдрическую группу входит 5 групп тетраэдрических.

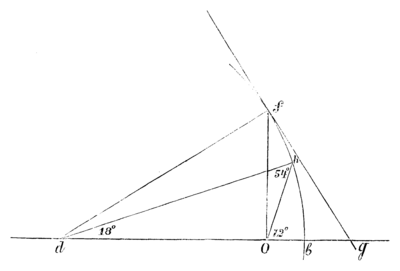
Поместим икосаэдр в сфере так, чтобы одна из осей, соединяющих две противоположные вершины его, совпала с осью сферы, а одна из плоскостей симметрии, проходящих через эту ось, прошла через действительную ось плоскости переменной $u$. Такое положение икосаэдра изображено на черт. 24.

В последующих вычислениях нам понадобится выражение линейной подстановки, соответствующей тому повороту сферы, который приводит икосаэдр из положения, изображенного на черт. 22, в положение, изображенное на черт. 24.

Полюсами оси вращения в данном случае служат точки $+i$ и $-i$. Вращение происходит около оси $AA'$ (черт. 22) в положительном направлении относительно наблюдателя, смотрящего от $A$ к $A'$. Угол поворота $\theta$ отмечен на чертеже 22 и определяется формулой:

$\operatorname {tg} \theta ={\frac {1}{2\cos \,36^{\circ }}}.$

(16)

‎Применяя формулы (39) и (41) главы III, находим, что искомая подстановка $\sigma$ выражается так:

$\sigma (u)={\frac {u+\operatorname {tg} {\dfrac {\theta }{2}}}{u\operatorname {tg} {\dfrac {\theta }{2}}-1}}.$

(17)

‎Обратная ей подстановка такова:

$\sigma ^{-1}(u)={\frac {u-\operatorname {tg} {\dfrac {\theta }{2}}}{u\operatorname {tg} {\dfrac {\theta }{2}}+1}}.$

(18)

Черт. 24

§ 15. Группа двупирамидная.

Углы треугольника двупирамидной группы суть: ${\frac {\pi }{m}},\ {\frac {\pi }{2}},\ {\frac {\pi }{2}}$, где $m$ — произвольное целое число^[6].

Черт. 25Поместим двупирамиду в сфере так, чтобы ось ее совпала с осью сферы и чтобы две вершины основания ее лежали симметрично относительно положительного направления действительной оси. Тогда сеть представляется в таком виде, как изображено на черт. 25 (чертеж этот соответствует случаю $m=5$).

Условимся называть сеть 25 нормальной двупирамидной сетью, соответствующую ей группу — нормальной двупирамидной группой.

Примем четырехугольник $0e^{-{\frac {\pi i}{m}}}1e^{\frac {\pi i}{m}}$ за основной четырехугольник сети.

Сопряженные стороны его суть: $0e^{-{\frac {\pi i}{m}}}$ и $0e^{\frac {\pi i}{m}}$, $1e^{-{\frac {\pi i}{m}}}$ и $1e^{\frac {\pi i}{m}}$.

Возьмем какую-нибудь точку $u$ на стороне $0e^{-{\frac {\pi i}{m}}}$ и соответствующую ей точку $u'$ на стороне $0e^{\frac {\pi i}{m}}$. Ясно, что

$u=\rho e^{-{\frac {\pi i}{m}}},\ u'=\rho e^{\frac {\pi i}{m}},$ где $0<\rho <1.$

‎Отсюда:

$u'=\varepsilon u,$ где $\varepsilon =e^{\frac {2\pi i}{m}}.$

(19)

‎Подстановка $S$, преобразующая сторону $0e^{-{\frac {\pi i}{m}}}$ в сопряженную с нею сторону $0e^{\frac {\pi i}{m}}$, выражается так:

$S(u)=\varepsilon u,$ где $\varepsilon =e^{\frac {2\pi i}{m}}.$

(20)

‎Возьмем точку $u$ на стороне $1e^{-{\frac {\pi i}{m}}}$ и соответствующую ей точку $u'$ на стороне $1e^{\frac {\pi i}{m}}$. Ясно, что

$u=e^{-\psi i},\ u'=e^{\psi i},$ где $0<\psi <{\frac {\pi i}{m}}.$

‎Отсюда:

$u'={\frac {1}{u}}.$

(21)

‎Подстановка ${\mathfrak {T}}$, преобразующая сторону $1e^{-{\frac {\pi i}{m}}}$ в сопряженную с ней сторону $1e^{\frac {\pi i}{m}}$, выражается так:

${\mathfrak {T}}(u)={\frac {1}{u}}.$

(22)

‎Для отличия символов подстановок двупирамидной группы от символов иных подстановок, мы присоединим к этим символам индекс «д» (двупирамида).

Итак, основные подстановки двупирамидной группы таковы:

$\left.{\begin{array}{l}S_{\text{д}}(u)=\varepsilon u,\ {\text{где}}\ \varepsilon =e^{\frac {2\pi i}{m}},\\{\mathfrak {T}}_{\text{д}}(u)={\dfrac {1}{u}}.\end{array}}\right\}$[7]

(23)

‎Первая из них $m$-го порядка, а вторая — 2-го порядка.

Первая из них соответствует повороту сферы на угол ${\frac {2\pi }{m}}$ около оси, соединяющей полюсы сферы, а вторая — повороту сферы на угол $\pi$ около действительной оси.

Вся совокупность $2m$ подстановок нормальной двупирамидной группы исчерпывается следующими формулами:

${\begin{matrix}\left.{\begin{array}{l}S_{\text{д}}^{k}(u)=\varepsilon ^{k}u,\\S_{\text{д}}^{k}{\mathfrak {T}}_{\text{д}}={\dfrac {\varepsilon ^{k}}{u}},\end{array}}\right\}&{\text{ где: }}&{\begin{array}{l}k=0,\ 1,\ 2,\ \ldots \ m-1,\\\varepsilon =e^{\frac {2\pi i}{m}}.\end{array}}\end{matrix}}$

(24)

‎Соответствие между этими подстановками и четырехугольниками сети указано на черт. 25.

Положив в предыдущих формулах $m=2$, найдем подстановки четверичной группы.

Основные подстановки ее суть:

$S_{\text{ч}}(u)=-u,\ {\mathfrak {T}}_{\text{ч}}(u)={\frac {1}{u}}.$

(25)

‎Они обе 2-го порядка.

Вся совокупность четырех подстановок нормальной четверичной группы такова:

$1\cdot u=u,\ S_{\text{ч}}(u)=-u,\ {\mathfrak {T}}_{\text{ч}}(u)={\frac {1}{u}},\ S_{\text{ч}}{\mathfrak {T}}_{\text{ч}}(u)=-{\frac {1}{u}}.$

(26)

Черт. 26‎Нормальная четверичная сеть изображена на черт. 26.

§ 16. Группа тетраэдрическая.

Треугольник тетраэдрической сети имеет углы, равные:

${\frac {\pi }{3}},\ {\frac {\pi }{3}},\ {\frac {\pi }{2}}.$^[8]

‎I. Дадим тетраэдру положение, изображенное на черт. 20: шесть середин ребер его лежат на осях координат.

Тетраэдрическую сеть, соответствующую такому положению тетраэдра, назовем первой нормальной тетраэдрической сетью.

В основном четырехугольнике $0acb$ сопряженные стороны суть: $0a$ и $0b$, $ca$ и $cb$.

Черт. 27

Возьмем пару соответственных точек $u$ и $u'$ на сторонах $0a$ и $0b$. Ясно, что:

$u=\rho e^{-{\frac {\pi i}{4}}},\ u'=-\rho e^{-{\frac {\pi i}{4}}},$

(27)

‎где $\rho$ меньше длины ${\overline {0a}}$^[9]:

$\rho <{\overline {0a}}.$

‎Из формул (27) следует, что:

$u'=-u.$

(28)

‎Подстановка ${\mathfrak {T}}$, преобразующая сторону $0a$ в $0b$, такова:

${\mathfrak {T}}(u)=-u.$

(29)

‎Возьмем пару соответственных точек $u$ и $u'$ на сторонах $ca$ и $cb$.

Не трудно видеть, что:

$u=-1+{\sqrt {2}}e^{\psi i},\ u'=-i+{\sqrt {2}}e^{\left({\frac {\pi }{2}}-\psi \right)i},$

(30)

‎где $\psi$ — переменная величина.

Из формул (30) следует:

$(u+1)(u'+i)=2i,$

‎откуда:

$u'=i{\frac {1-u}{1+u}}.$

(31)

‎Подстановка $S$, преобразующая сторону $ca$ в сопряженную с ней $cb$, такова:

$S(u)=i{\frac {1-u}{1+u}}.$

(32)

‎Подстановки $S$ и ${\mathfrak {T}}$ суть основные подстановки первой нормальной тетраэдрической группы.

Укажем на одну простую неосновную подстановку этой группы: вычислим коэффициенты подстановки, преобразующей треугольник $0ac$ в треугольник $\infty df$.

Соответственные вершины этих треугольников суть: 0 и $\infty$, $a$ и $d$, $c$ и $f$.

Подстановка, преобразующая точки $0,\ a,\ c$ соответственно в $\infty ,\ d,\ f$, и есть искомая подстановка — этими условиями она определена вполне.

Весьма простыми вычислениями находим, что:

${\begin{array}{ll}a={\dfrac {{\sqrt {6}}-{\sqrt {2}}}{2}}e^{-{\frac {\pi i}{4}}},&c={\dfrac {{\sqrt {6}}-{\sqrt {2}}}{2}}e^{\frac {\pi i}{4}},\\d={\dfrac {{\sqrt {6}}+{\sqrt {2}}}{2}}e^{\frac {\pi i}{4}},&f={\dfrac {{\sqrt {6}}+{\sqrt {2}}}{2}}e^{-{\frac {\pi i}{4}}}.\end{array}}$

(33)

‎Отсюда следует:

$ad=1,\ cf=1.$

‎или:

$d={\frac {1}{a}},\ f={\frac {1}{c}}.$

(34)

‎Так как, кроме того, мы вправе написать:

$\infty ={\frac {1}{0}},$

‎то мы приходим к заключению, что подстановка $U$, преобразующая треугольник $0ac$ в $\infty df$, такова:

$U(u)={\frac {1}{u}},$

(35)

‎Для отличия символов подстановок тетраэдрической группы от символов иных подстановок, мы будем отмечать их индексом «т» (тетраэдр).

Итак, мы нашли две основные подстановки первой нормальной тетраэдрической группы:

$\left.{\begin{array}{l}S_{\text{т}}(u)=i{\dfrac {1-u}{1+u}},\\{\mathfrak {T}}_{\text{т}}(u)=-u,\end{array}}\right\}$

(36)

‎и одну весьма простую неосновную подстановку:

$U_{\text{т}}(u)={\frac {1}{u}}.$

(37)

Подстановка $S_{\text{т}}$ — третьего порядка, ${\mathfrak {T}}_{\text{т}}$ и $U_{\text{т}}$ — второго порядка.

Все 12 подстановок 1-ой нормальной тетраэдрической группы исчерпываются следующими формулами:

$\left.{\begin{matrix}1\,.\,u=u,\ S_{\text{т}}(u)=i{\dfrac {1-u}{1+u}},\ S_{\text{т}}^{2}(u)={\dfrac {i-u}{i+u}},\\{\mathfrak {T}}_{\text{т}}(u)=-u,\ {\mathfrak {T}}_{\text{т}}S_{\text{т}}(u)=-i{\dfrac {1-u}{1+u}},\\{\mathfrak {T}}_{\text{т}}S_{\text{т}}^{2}(u)=-{\dfrac {i-u}{i+u}},\\U_{\text{т}}(u)={\dfrac {1}{u}},\ U_{\text{т}}S_{\text{т}}(u)=-i{\dfrac {1+u}{1-u}},\\U_{\text{т}}S_{\text{т}}^{2}(u)={\dfrac {i+u}{i-u}},\\{\mathfrak {T}}_{\text{т}}U_{\text{т}}(u)=-{\dfrac {1}{u}},\ {\mathfrak {T}}_{\text{т}}U_{\text{т}}S_{\text{т}}(u)=i{\dfrac {1+u}{1-u}},\\{\mathfrak {T}}_{\text{т}}U_{\text{т}}S_{\text{т}}^{2}(u)=-{\dfrac {i+u}{i-u}}.\end{matrix}}\right\}$

(38)

‎Соответствие между подстановками группы и четырехугольниками сети указано на черт. 27.

Из этого чертежа, между прочим, видно, что

$U_{\text{т}}(u)=S_{\text{т}}^{2}{\mathfrak {T}}_{\text{т}}S_{\text{т}},$

(39)

‎в чем также очень легко убедиться поверкой при помощи формул (38).

Из чертежа 27 видно, что подстановка ${\mathfrak {T}}_{\text{т}}S_{\text{т}}$ есть эллиптическая подстановка, соответствующая повороту сферы на угол ${\frac {2\pi }{3}}$ около оси, один из полюсов которой проектируется в точку $a$.

Следовательно это подстановка 3-го порядка:

${\mathfrak {T}}_{\text{т}}S_{\text{т}}{\mathfrak {T}}_{\text{т}}S_{\text{т}}{\mathfrak {T}}_{\text{т}}S_{\text{т}}=1.$

(40)

‎Символических соотношений, подобных (40), можно вывести довольно много, пользуясь чертежем 27, но они нам в дальнейшем не будут нужны.

Обратим внимание на то, что все подстановки четверичной группы (26) входят в состав тетраэдрической группы (38):

$S_{\text{ч}}={\mathfrak {T}}_{\text{т}},\ {\mathfrak {T}}_{\text{ч}}=U_{\text{т}}.$

(41)

‎Чтобы из четверичной группы получить тетраэдрическую, мы должны к подстановкам четверичной группы присоединить их комбинации с тетраэдрическими подстановками:

$S_{\text{т}},\ S_{\text{т}}^{2}.$

‎Преобразуя^[10] четверичную группу посредством подстановок $S_{\text{т}}$ и $S_{\text{т}}^{2}$, мы снова получаем ту же четверичную группу. Следовательно четверичная группа есть особая часть тетраэдрической.

Отношение порядков этих групп (показатель сложности) равно 3.

Отсюда следует, что функция, инвариантная относительно подстановок четверичной группы, выражается рационально через функцию, инвариантную относительно подстановок тетраэдрической группы; а эта последняя функция выражается через первую при посредстве одного кубического радикала. Эти формулы мы построим в главе VII, и они дадут нам возможность решить в радикалах тетраэдрическое уравнение.

II. Построим теперь сеть, соответствующую другому положению тетраэдра в сфере: поместим тетраэдр в сфере так, чтобы одна вершина его лежала в северном полюсе сферы и чтобы одно из ребер его пересекало положительное направление действительной оси. Сеть, соответствующая такому положению тетраэдра, изображена на черт. 28.

Черт. 28Такую сеть мы условимся называть второй нормальной тетраэдрической сетью, а соответствующую ей группу — второй нормальной тетрадэрической группой.

Примем $0abc$ за основной четырехугольник сети 28.

Сопряженные стороны его суть: $0a$ и $0c$, $ba$ и $bc$.

Пользуясь теми же приемами, которые мы прилагали выше, мы находим, что подстановка $S'_{\text{т}}$, преобразующая сторону $0a$ в $0c$, выражается так:

$S'_{\text{т}}(u)=\varepsilon u,$ где $\varepsilon =e^{\frac {2\pi i}{3}};$

(42)

‎подстановка же ${\mathfrak {T}}'_{\text{т}}(u)$, преобразующая сторону $ba$ в $bc$, такова:

${\mathfrak {T}}'_{\text{т}}(u)={\frac {{\sqrt {2}}-u}{{\sqrt {2}}u+1}}.$[11]

(43)

‎III. Возьмем тетраэдр в положении, соответствующем первой нормальной группе и построим соответствующий ему икосаэдр: он изображен на черт. 22. Повернем икосаэдр вместе с тетраэдром около мнимой оси плоскости на угол $\theta$, отмеченный на чертеже 22. Икосаэдр примет положение, изображенное на черт. 24, а тетраэдр — некоторое новое положение, нами еще не рассмотренное.

Сеть, соответствующая такому положению тетраэдра, условимся называть третьей нормальной тетраэдрической сетью.

Из сказанного следует, что первая нормальная тетраэдрическая сеть преобразуется в 3-ю посредством подстановки $\sigma$, выражаемой формулами (17) и (16).

Третья нормальная тетраэдрическая группа будет иметь для нас лишь вспомогательное значение при сравнении форм икосаэдрического типа с формами типа тетраэдрического.

Поэтому мы не будем теперь вычислять основных подстановок этой группы и только обозначим их буквами:

$S''_{\text{т}}$ и ${\mathfrak {T}}''_{\text{т}}.$

‎§ 17. Группа октаэдрическая.

Углы треугольника октаэдрической сети суть: ${\frac {\pi }{4}},\ {\frac {\pi }{3}},\ {\frac {\pi }{2}}.$

I. Возьмем октаэдр в положении, изображенном на черт. 21: его вершины лежат на осях координат, к которым отнесена сфера.

Сеть, соответствующую такому положению октаэдра, мы назовем первой нормальной октаэдрической сетью. Она изображена на черт. 29.

Примем за основной четырехугольник ее $0abc$. Сопряженные стороны его суть: $0a$ и $0c$, $ba$ и $bc$. Основные подстановки $S_{\text{о}}$ и ${\mathfrak {T}}_{\text{о}}$, преобразующие $0a$ в $0c$ и $ba$ в $bc$, выражаются так:

$\left.{\begin{array}{l}S_{\text{о}}(u)=iu,\\{\mathfrak {T}}_{\text{о}}={\dfrac {1-u}{1+u}}.\end{array}}\right\}$[12]

(44)

Формулы (44) дают выражения основных подстановок первой нормальной октаэдрической группы.

Черт. 29

Первая из них 4-го, а вторая — 2-го порядка.

Укажем на одну весьма простую неосновную подстановку, преобразующую треугольник $0bc$ в $\infty df$. Применяя совершенно такие же рассуждения, как и в § 16, находим, что искомая подстановка выражается так:

$U_{\text{о}}(u)={\frac {1}{u}}.$

(45)

‎Вся совокупность 24 подстановок первой нормальной октаэдрической группы исчерпывается формулами:

$\left.{\begin{array}{l}\quad \quad \quad S_{\text{о}}^{k}(u)=i^{k}u,\\\quad \quad \quad S_{\text{о}}^{k}(u){\mathfrak {T}}_{\text{о}}S_{\text{о}}^{h}(u)=i^{k}{\dfrac {1-i^{h}u}{1+i^{h}u}},\\\quad \quad \quad S_{\text{о}}^{k}(u)U_{\text{о}}(u)={\dfrac {i^{k}}{u}},\\{\text{где:}}\\\quad \quad \quad k,\;h=0,\;1,\;2,\;3.\end{array}}\right\}$

(46)

‎Соответствие между подстановками группы и четырехугольниками сети указано на самом черт. 29. Из черт. 29 видно, что подстановка $U_{\text{о}}$ выражается через основные подстановки $S_{\text{о}}$ и ${\mathfrak {T}}_{\text{о}}$ формулой:

$U_{\text{о}}={\mathfrak {T}}_{\text{о}}S_{\text{о}}^{2}{\mathfrak {T}}_{\text{о}},$

(47)

‎в чем легко убедиться и непосредственной поверкой. Из черт. 29, между прочим, видно, что подстановка $S_{\text{о}}{\mathfrak {T}}_{\text{о}}$ соответствует повороту сферы на угол ${\frac {2\pi }{3}}$ около оси, один из полюсов которой проектируется в точку $c$. Следовательно $S_{\text{о}}{\mathfrak {T}}_{\text{о}}$ есть эллиптическая подстановка 3-го порядка:

$S_{\text{о}}{\mathfrak {T}}_{\text{о}}S_{\text{о}}{\mathfrak {T}}_{\text{о}}S_{\text{о}}{\mathfrak {T}}_{\text{о}}=1.$

(48)

‎Сравнивая октаэдрическую группу (46) с тетраэдрической группой (38), мы замечаем, что основные подстановки тетраэдрической группы входят в октаэдрическую:

$S_{\text{т}}=S_{\text{о}}{\mathfrak {T}}_{\text{о}},\ {\mathfrak {T}}_{\text{т}}=S_{\text{о}}^{2}.$

(49)

‎Чтобы из тетраэдрической группы получить октаэдрическую, мы должны присоединить к подстановкам тетраэдрической группы комбинации этих подстановок с октаэдрической подстановкой $S_{\text{о}}$. Преобразуя тетраэдрическую группу подстановкой $S_{\text{о}}$, мы опять получаем ту же тетраэдрическую группу. Следовательно тетраэдрическая группа есть особая часть октаэдрической. Отношение порядков этих групп (показатель сложности) равно 2.

Отсюда следует, что всякая функция, инвариантная по отношению к подстановкам октаэдрической группы, выражается рационально через функцию, инвариантную по отношению к подстановкам группы тетраэдрической; обратно же — вторая функция выражается через первую при помощи одного квадратного радикала. Эти формулы мы построим в главе VII. Благодаря им, умея решить в радикалах тетраэдрическое уравнение, мы будем в состоянии решить в радикалах также и уравнение октаэдрическое.

II. Возьмем тетраэдр в положении, соответствующем 2-ой нормальной тетраэдрической сети, и соответствующий ему октаэдр.

Черт. 30

Два противоположных центра граней его поместятся в полюсах сферы. Сеть, соответствующая такому положению октаэдра, изображена на черт. 30.

Сеть, определяемую этими условиями, мы назовем второй нормальной октаэдрической сетью.

Примем за основной четырехугольник $0gbf$.

Сопряженные стороны его суть: $0g$ и $0f$, $bg$ и $bf$. Подстановки $S'_{\text{о}}$ и ${\mathfrak {T}}'_{\text{о}}$^[13], преобразующие $0g$ в $0f$ и $bg$ в $bf$, выражаются так:

${\begin{matrix}\left.{\begin{array}{l}S'_{\text{о}}(u)=\varepsilon u,\\{\mathfrak {T}}'_{\text{о}}={\dfrac {1+{\sqrt {2}}\varepsilon ^{2}u}{u-{\sqrt {2}}\varepsilon }},\end{array}}\right\}&{\text{где}}&\varepsilon =e^{\frac {2\pi i}{3}}.\end{matrix}}$[14]

(50)

‎Ясно, что сеть 30 может быть получена из сети 29 тем же линейным преобразованием, которое сеть 27 преобразует в сеть 28.

III. Возьмем тетраэдр в положении, соответствующем третьей нормальной тетраэдрической сети, и построим соответствующий ему октаэдр. Сеть, соответствующую такому положению октаэдра, назовем третьей нормальной октаэдрической сетью. Она получается из 1-ой нормальной октаэдрической сети преобразованием посредством подстановки $\sigma$, где $\sigma$ есть линейная подстановка (17), найденная в § 14.

Основные подстановки третьей нормальной октаэдрической группы мы будем обозначать так:

$S'_{\text{о}}$ и ${\mathfrak {T}}'_{\text{о}}.$

‎Долее на этой группе мы не останавливаемся потому, что она будет иметь для нас лишь вспомогательное значение.

§ 18. Группа икосаэдрическая.

I. Поместим икосаэдр в сфере так, как изображено на черт. 24. Сеть, соответствующую такому положению икосаэдра, назовем первой нормальной икосаэдрической сетью.

Она изображена на чертеже I^[15].

За основную область икосаэдрической группы мы примем четырехугольник $0abc$. Сопряженные стороны его суть: $0a$ и $0c$, $ba$ и $bc$.

Подстановка $S_{\text{и}}$, преобразующая сторону $0a$ в $0c$, как легко видеть, такова:

$S_{\text{и}}=\varepsilon u,$ где $\varepsilon =e^{\frac {2\pi i}{5}}.$

(51)

‎Подстановка ${\mathfrak {T}}_{\text{и}}$, преобразующая сторону $ba$ в $bc$, получается тем же способом, но вычисления несколько сложнее. Рассмотрим эти вычисления подробно.

Черт. 31

Для ясности некоторые части чертежа I изображены в большем масштабе на черт. 31.

Точка $f$ лежит на экваторе сферы; поэтому:

${\overline {0f}}=1.$

Из черт. I видно, что:

${\overline {0h}}={\overline {0g}},\;{\overline {df}}={\overline {dh}}.$

‎Прямая $0f$ перпендикулярна к $dg$.

Из треугольника $dh0$ (черт. 31) находим:

${\overline {0h}}={\overline {d0}}{\frac {\sin 18^{\circ }}{\sin 54^{\circ }}}.$

‎Из прямоугольного треугольника $dfg$ находим:

${\overline {f0}}^{2}={\overline {d0}}\cdot {\overline {0g}}.$

‎Из сказанного следует:

$1={\overline {d0}}^{2}{\frac {\sin 18^{\circ }}{\sin 54^{\circ }}},\;{\overline {d0}}={\frac {{\sqrt {5}}+1}{2}},\;{\overline {b0}}={\frac {{\sqrt {5}}-1}{2}};$

‎далее:

${\overline {df}}={\sqrt {{\overline {d0}}\cdot {\overline {dg}}}}={\sqrt {\frac {5+{\sqrt {5}}}{2}}}.$

‎Взяв пару соответственных точек $u$ и $u'$ на сопряженных сторонах $ba$ и $bc$, находим:

$\left.{\begin{array}{l}u=-{\dfrac {{\sqrt {5}}+1}{2}}+{\sqrt {\dfrac {5+{\sqrt {5}}}{2}}}e^{-\psi i},\\u'=-{\dfrac {{\sqrt {5}}+1}{2}}+{\sqrt {\dfrac {5+{\sqrt {5}}}{2}}}e^{\psi i},\end{array}}\right\}$

(52)

‎где $\psi$ — переменная величина.

Отсюда:

$\left(u+{\frac {{\sqrt {5}}+1}{2}}\right)\left(u'+{\frac {{\sqrt {5}}+1}{2}}\right)={\frac {5+{\sqrt {5}}}{2}}.$

(53)

‎Так как:

$-{\frac {{\sqrt {5}}+1}{2}}=\varepsilon ^{2}+\varepsilon ^{3},$ где $\varepsilon =e^{\frac {2\pi i}{5}},$

‎то из уравнения (53), находим:

$u'={\frac {1+(\varepsilon ^{2}+\varepsilon ^{3})u}{u-(\varepsilon ^{2}+\varepsilon ^{3})}}.$

(54)

‎Искомая подстановка ${\mathfrak {T}}_{\text{и}}(u)$ выражается так:

${\mathfrak {T}}_{\text{и}}(u)={\frac {1+(\varepsilon ^{2}+\varepsilon ^{3})u}{u-(\varepsilon ^{2}+\varepsilon ^{3})}}.$

(55)

‎Основные подстановки 1-ой нормальной икосаэдрической группы суть:

$\left.{\begin{array}{l}S_{\text{и}}(u)=\varepsilon u,\\{\mathfrak {T}}_{\text{и}}(u)={\dfrac {1+(\varepsilon ^{2}+\varepsilon ^{3})u}{u-(\varepsilon ^{2}+\varepsilon ^{3})}},\\{\text{где }}\varepsilon =e^{\frac {2\pi i}{5}}.\end{array}}\right\}$

(56)

‎Первая из них 5-го, а вторая — 2-го порядка.

Обратим внимание на одну очень простую неосновную подстановку $U_{\text{и}}$, преобразующую треугольник $0bc$ в эквивалентный ему треугольник $\infty kl$. Соответственные вершины этих треугольников суть: 0 и $\infty$, $b$ и $k$, $c$ и $l$. Рассуждениями, подобными приведенным в § 16, находим, что искомая подстановка $U_{\text{и}}$ выражается так:

$U_{\text{и}}(u)=-{\frac {1}{u}}.$

(57)

‎Вся совокупность 60 подстановок первой нормальной икосаэдрической группы исчерпывается формулами:

$\left.{\begin{array}{l}S_{\text{и}}^{k}(u)=\varepsilon ^{k}u,\;S_{\text{и}}^{k}U_{\text{и}}(u)=-{\dfrac {\varepsilon ^{k}}{u}},\\S_{\text{и}}^{k}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{h}(u)=\varepsilon ^{k}{\dfrac {1+(\varepsilon ^{2}+\varepsilon ^{3})\varepsilon ^{h}u}{\varepsilon ^{h}u-(\varepsilon ^{2}+\varepsilon ^{3})}},\\S_{\text{и}}^{k}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{h}U_{\text{и}}=-{\dfrac {u-(\varepsilon ^{2}+\varepsilon ^{3})\varepsilon ^{h}}{\varepsilon ^{h}+(\varepsilon ^{2}+\varepsilon ^{3})u}},\\{\text{где }}k,\;h=0,\;1,\;2,\;3,\;4.\end{array}}\right\}$

(58)

‎Соответствия между подстановками группы и четырехугольниками икосаэдрической сети указаны на чертеже I.

Из чертежа I видно, что

$U=S_{\text{и}}^{2}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{3}{\mathfrak {T}}_{\text{и}}S_{\text{и}}^{2}{\mathfrak {T}}_{\text{и}}.$

(59)

‎Кроме того мы замечаем, что подстановка $S_{\text{и}}{\mathfrak {T}}_{\text{и}}$ соответствует повороту сферы на угол ${\frac {2\pi }{3}}$ около оси, один из полюсов которой проектируется в точку $c$. Следовательно подстановка

$S_{\text{и}}{\mathfrak {T}}_{\text{и}}$

‎— третьего порядка:

$S_{\text{и}}{\mathfrak {T}}_{\text{и}}S_{\text{и}}{\mathfrak {T}}_{\text{и}}S_{\text{и}}{\mathfrak {T}}_{\text{и}}=1.$

(60)

‎II. Возьмем икосаэдр в положении, указанном на черт. 22.

Сеть, соответствующую такому положению икосаэдра, мы назовем второй нормальной икосаэдрической сетью. Она изображена на чертеже II^[16]. Ясно, что эта сеть может быть получена из первой преобразованием посредством подстановки $\sigma ^{-1}$, определяемой формулой (18).

Подстановки второй нормальной икосаэдрической группы мы не вычисляем, потому что они нам нужны не будут.

---

Выше мы видели, что положение икосаэдра не меняется от поворотов, не меняющих положения соответствующего ему тетраэдра. Отсюда следует, что в первую нормальную икосаэдрическую группу входит третья нормальная тетраэдрическая группа, а во вторую нормальную икосаэдрическую группу входит первая нормальная тетраэдрическая группа.

Тетраэдрическая группа, входящая в икосаэдрическую, не составляет собой части ее. В этом кроется существенное различие икосаэдрической группы от остальных рассмотренных нами групп. В главе VII мы увидим, что вследствие сказанной особенности икосаэдрической группы, икосаэдрическое уравнение неразрешимо в радикалах.

§ 19. Циклическая группа конечного порядка.

Циклическая группа состоит из степеней одной и той же подстановки:

$S^{0},\;S^{1},\;S^{2},\;S^{3},\;\ldots$

(61)

‎Она может быть конечного порядка только тогда, когда подстановка $S$ есть эллиптическая подстановка конечного порядка. Порядок группы (61) равен порядку подстановки $S$.

Возьмем сначала эллиптическую подстановку конечного порядка $m$ в нормальной форме:

$S'(u)=e^{\frac {2h\pi i}{m}}u,$

(62)

‎где $k$ и $m$ — числа взаимно простые.

Взяв наименьший положительный корень $\alpha$ сравнения:

$h\alpha \equiv 1{\pmod {m}},$

(63)

‎мы найдем:

$S'^{\,\alpha }(u)=e^{\frac {2\pi i}{m}}u.$

(64)

‎Итак, в рассматриваемую циклическую группу входит подстановка:

$S(u)=e^{\frac {2\pi i}{m}}u,$

(65)

‎или, короче:

$S(u)=\varepsilon u,$ где $\varepsilon =e^{\frac {2\pi i}{m}}.$

(66)

‎Группа может быть представлена в таком виде:

$S^{0}=1,\;S,\;S^{2},\;\ldots ,\;S^{m-1}.$

(67)

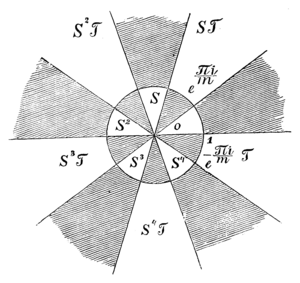
‎Не трудно убедиться в том, что основная область этой группы может быть представлена в виде бесконечной части плоскости ограниченной двумя прямыми, выходящими из начала координат и наклоненными друг к другу под углом ${\frac {2\pi }{m}}$.

Черт. 32Покрыв всю плоскость сетью таких областей, как указано на черт. 32, мы получим сеть, которая соответствует нормальной циклической группе (67) в том же самом смысле, в каком рассмотренные выше сети четырехугольников соответствовали группам: двупирамидной, тетраэдрической и т. д.

Действительно, если мы возьмем в какой-либо из $m$ областей произвольную точку $u$, то в каждой из остальных областей найдется единственная эквивалентная ей точка относительно подстановок циклической группы (67).

Если мы хотим построить какую-нибудь (не нормальную) циклическую сеть, то должны преобразовать сеть 32 какой-нибудь линейной подстановкой. При этом точки $O$ и $\infty$ преобразуются в некоторые две, вообще говоря, конечные точки $a$ и $b$, а лучи, идущие на черт. 32 из точки $O$ в бесконечность, преобразуются в дуги кругов, соединяющие точки $a$ и $b$. Получится сеть, изображенная на черт. 33. Основная подстановка ${\bar {S}}$ этой группы есть та подстановка, которая преобразует одну из дуг, напр., $acb$ в ближайшую следующую за ней: в $adb$. Группа, соответствующая сети 33, представится в таком виде:

${\bar {S}}^{0}=1,\;{\bar {S}},\;{\bar {S}}^{2},\ldots \;{\bar {S}}^{m-1}.$

(68)

Черт. 33

Основная область циклической группы имеет вид двуугольника $acbda$, как мы уже замечали выше.

Так как всякая группа содержит в себе все степени всякой подстановки, входящей в эту группу, то циклическая группа входит во всякую группу.

§ 20. Конечные группы бинарных линейных подстановок.

Бинарной подстановкою, как мы уже говорили в главе I, мы называем преобразование двух переменных $y_{1},\ y_{2}$ такого вида:

$\left.{\begin{array}{l}{\bar {y}}_{1}=\alpha y_{1}+\beta y_{2},\\{\bar {y}}_{2}=\gamma y_{1}+\delta y_{2},\end{array}}\right\}$

(69)

‎где $\alpha ,\ \beta ,\ \gamma ,\ \delta$ — какие-либо постоянные числа. Для краткости мы будем обозначать бинарную подстановку (69) таким символом:

${\begin{pmatrix}\alpha ,&\beta \\\gamma ,&\delta \end{pmatrix}}.$

(70)

‎Определителем бинарной линейной подстановки (70) называется величина:

$\alpha \delta -\beta \gamma .$

‎Перемножив символически две линейные бинарные подстановки, мы получаем опять линейную бинарную подстановку, определитель которой равен произведению определителей перемноженных подстановок.

Если некоторая совокупность линейных бинарных подстановок образует группу^[17], то мы назовем ее группой бинарных подстановок.

Каждой бинарной линейной подстановке (70) соответствует единственная неоднородная линейная подстановка:

${\bar {u}}={\frac {\alpha u+\beta }{\gamma u+\delta }},$

(71)

‎но не обратно: каждой неоднородной подстановке (71) соответствует бесконечное множество бинарных подстановок, которые можно изобразить символом:

${\begin{pmatrix}\rho \alpha ,&\rho \beta \\\rho \gamma ,&\rho \delta \end{pmatrix}},$

(72)

‎где $\rho$ — произвольная постоянная.

Если две группы одинакового порядка составлены из одинакового числа основных подстановок так, что каждой подстановке одной группы соответствует единственная подстановка другой, и обратно, то мы назовем их изоморфными группами^[18].

Возьмем группу $\Gamma$ бинарных линейных подстановок, найдем соответствующие им неоднородные линейные подстановки. Эти последние, конечно, образуют некоторую группу $G$ неоднородных линейных подстановок.

Если порядок группы $\Gamma$ конечный, то и порядок группы $G$ будет конечный. Эта группа будет принадлежать к одному из типов: циклическому, двупирамидному, тетраэдрическому, октаэдрическому или икосаэдрическому.

Посмотрим, могут ли быть группы $\Gamma$ и $G$ изоморфны между собой.

Для простоты мы можем предполагать группу $G$, приведенной к нормальному виду^[19].

I. Пусть $G$ группа циклическая и пусть она изоморфна соответствующей ей группе $\Gamma$.

Группа $G$ составлена из одной основной подстановки:

$S(u)=\varepsilon u,$ где $\varepsilon =e^{\frac {2\pi i}{m}}.$

(66)

‎Соответствующая ей основная бинарная подстановка группы $\Gamma$ такова:

${\begin{pmatrix}\rho \varepsilon ,&0\\0,&\rho \end{pmatrix}},$

(73)

‎где $\rho$ — некоторый постоянный множитель.

Так как

$S^{m}=1,$

(74)

‎то должно иметь место символическое равенство:

$\sigma ^{m}=1,$

(75)

‎или:

${\begin{pmatrix}\rho ^{m}\varepsilon ^{m},&0\\0,&\rho ^{m}\end{pmatrix}},$

(76)

‎откуда:

$\rho ^{m}=1.$

(77)

‎Если $\rho$ есть корень $m$-ой степени из 1, то циклическая группа бинарных линейных подстановок:

$\sigma ^{0}=1,\;\sigma ,\;\sigma ^{2},\;\ldots ,\;\sigma ^{m-1}$

(78)

‎изоморфна группе неоднородных линейных подстановок:

$S^{0}=1,\;S,\;S^{2},\;\ldots ,\;S^{m-1}.$

(67)

‎II. Пусть группа $G$ двупирамидная и изоморфна соответствующей ей группе $\Gamma$.

Основные подстановки двупирамидной группы суть:

$\left.{\begin{array}{l}S_{\text{д}}(u)=\varepsilon u,\ {\text{где}}\ \varepsilon =e^{\frac {2\pi i}{m}},\\{\mathfrak {T}}_{\text{д}}(u)={\dfrac {1}{u}}.\end{array}}\right\}$

(23)

‎Основные подстановки группы $\Gamma$ суть:

$\sigma ={\begin{pmatrix}\rho \varepsilon ,&0\\0,&\rho \end{pmatrix}},\;\tau ={\begin{pmatrix}0,&\rho '\\\rho ',&0\end{pmatrix}}.$

(79)

‎Так как:

$S^{m}=1,\;{\mathfrak {T}}^{2}=1,$

(80)

‎то должны иметь место символические равенства:

$\sigma ^{m}=1,\;\tau ^{2}=1,$

(81)

‎или:

${\begin{pmatrix}\rho ^{m}\varepsilon ^{m},&0\\0,&\rho ^{m}\end{pmatrix}}=1,\;{\begin{pmatrix}0,&\rho '^{\,2}\\\rho '^{\,2},&0\end{pmatrix}}=1,$

(82)

‎откуда:

$\rho ^{m}=1,\;\rho '^{\,2}=1.$

(83)

‎В группу $G$ входит подстановка 2-го порядка $S{\mathfrak {T}}$:

$S{\mathfrak {T}}(u)={\frac {\varepsilon }{u}}.$

(84)

‎Соответствующая ей подстановка $\sigma \tau$ тоже должна быть второго порядка:

$(\sigma \tau )^{2}={\begin{pmatrix}0,&\rho \rho '\varepsilon \\\rho \rho ',&0\end{pmatrix}}^{2}={\begin{pmatrix}\rho ^{2}\rho '^{\,2}\varepsilon ,&0\\0,&\rho ^{2}\rho '^{\,2}\varepsilon \end{pmatrix}}=1,$

(85)

‎откуда:

$\rho ^{2}\rho '^{\,2}\varepsilon =1.$

(86)

‎Из равенств (83) и (86) следует:

$\rho ^{2}=e^{-{\frac {2\pi i}{m}}},$

(87)

‎откуда:

$\rho =\pm e^{-{\frac {\pi i}{m}}},$

(88)

‎и далее:

$\rho ^{m}=-(\pm 1)^{m}.$

(88)

‎Ясно, что последнее равенство не противоречит первому из равенств (83) только в том случае, если $m$ нечетно и если, кроме того, в формуле (88) взят нижний знак. В таком случае имеем:

$\rho =-e^{-{\frac {\pi i}{m}}}.$

(90)

‎Итак, двупирамидная группа бинарных линейных подстановок только в том случае может быть изоморфна соответствующей ей группе неоднородных линейных подстановок, если порядок этой группы есть число вида:

$2m=2(2p+1).$

III. Пусть группа $G$ тетраэдрическая, октаэдрическая или икосаэдрическая.

Мы уже видели выше, что в состав каждой из этих групп входит группа четверичная, то есть двупирамидная, порядка

$2m=2\cdot 2.$

‎Эта четверичная группа на основании только что полученного результата не может быть изоморфна соответствующей ей группе бинарных линейных подстановок.

Если так, то и вся группа $G$ не может быть изоморфна группе $\Gamma$.

Этот последний результат можно формулировать в виде такой теоремы:

Теорема 4. Группы бинарных подстановок тетраэдрического, октаэдрического и икосаэдрического типов не могут быть изоморфны группам соответствующих им неоднородных линейных подстановок.

Теорема эта принадлежит Клейну^[20] и имеет важное значение для изучаемых нами уравнений.

Пользуясь теоремой 4, мы можем несколько пополнить результаты главы I.

Мы знаем из теоремы 8 главы I, что существует группа бинарных линейных подстановок с определителем равным 1, связывающая между собой корни уравнения (20) главы I.

Порядок этой группы равен степени $n$ уравнения (20) главы I. Подстановки этой группы выражают каждый корень уравнения (20) через два корня того же уравнения.

Далее, из теоремы 22 главы I мы знаем, что отношения корней уравнения (20) служат корнями уравнения (95) степени $N$, причем $N$ равно $n$ или ${\frac {n}{2}}$. Уравнение (95) главы I имеет группу неоднородных линейных подстановок, соответствующую группе бинарных линейных подстановок уравнения (20).

Ясно, что степень $N$ уравнения (95) может равняться степени $n$ уравнения (20) только в том случае, когда две названные группы изоморфны, а это возможно только для двупирамидной группы, степень которой есть число вида:

$2m=2(2p+1).$

‎Итак, для типов: тетраэдрического, октаэдрического и икосаэдрического степень $n$ уравнения (20) вдвое выше степени $N$ уравнения (95):

$n=2N.$

‎Отсюда следует, что в формулах (106) и (107) главы I радикал не может быть извлечен точно из подкоренных выражений; корни уравнения (20) попарно разнятся знаками.

Посмотрим, каковы группы уравнений (20) главы I для каждого из 4 типов.

Это суть группы бинарных подстановок с определителем 1, соответствующие группам неоднородных линейных подстановок, найденным в настоящей главе.

Имея неоднородную подстановку

${\bar {u}}={\frac {\alpha u+\beta }{\gamma u+\delta }},$

‎легко найти соответствующие ей бинарные подстановки с определителем 1. Это суть подстановки вида:

${\begin{pmatrix}\rho \alpha ,&\rho \beta \\\rho \gamma ,&\rho \delta \end{pmatrix}},$

‎где $\rho$ есть величина, определяемая условием:

$\rho ^{2}(\alpha \delta -\beta \gamma )=1.$

‎Ясно, что $\rho$ имеет два значения, разнящихся знаками.

Выполним эти вычисления для первых нормальных групп, найденных в настоящей главе.

В результате мы найдем такие выражения основных подстановок конечных групп бинарных линейных подстановок:

Группа двупирамидная.

$\sigma ={\begin{pmatrix}e^{\frac {\pi i}{m}},&0\\0,&e^{-{\frac {\pi i}{m}}}\end{pmatrix}},\;\tau ={\begin{pmatrix}0,&i\\i,&0\end{pmatrix}}.$

(91)

Группа тетраэдрическая.

$\sigma ={\begin{pmatrix}{\dfrac {e^{-{\frac {\pi i}{4}}}}{\sqrt {2}}},&{\dfrac {e^{\frac {3\pi i}{4}}}{\sqrt {2}}}\\{\dfrac {e^{\frac {\pi i}{4}}}{\sqrt {2}}},&{\dfrac {e^{\frac {\pi i}{4}}}{\sqrt {2}}}\end{pmatrix}},\;\tau ={\begin{pmatrix}i,&0\\0,&-i\end{pmatrix}}.$

(92)

Группа октаэдрическая.

$\sigma ={\begin{pmatrix}e^{\frac {\pi i}{4}},&0\\0,&e^{-{\frac {\pi i}{4}}}\end{pmatrix}},\;\tau ={\begin{pmatrix}-{\dfrac {i}{\sqrt {2}}},&{\dfrac {i}{\sqrt {2}}}\\{\dfrac {i}{\sqrt {2}}},&{\dfrac {i}{\sqrt {2}}}\end{pmatrix}}.$

(93)

Группа икосаэдрическая.

$\sigma ={\begin{pmatrix}-\varepsilon ^{3},&0\\0,&-\varepsilon ^{2}\end{pmatrix}},\;\tau ={\begin{pmatrix}-{\dfrac {\varepsilon -\varepsilon ^{4}}{\sqrt {5}}},&{\dfrac {\varepsilon ^{2}-\varepsilon ^{3}}{\sqrt {5}}}\\{\dfrac {\varepsilon ^{2}-\varepsilon ^{3}}{\sqrt {5}}},&{\dfrac {\varepsilon -\varepsilon ^{4}}{\sqrt {5}}}\end{pmatrix}},$ где $\varepsilon =e^{\frac {2\pi i}{5}}.$

(94)

‎Не трудно усмотреть, что во все четыре группы входит подстановка:

${\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

(95)

‎т. е.

$\left.{\begin{array}{l}{\bar {y}}_{1}=-y_{1},\\{\bar {y}}_{2}=-y_{2}.\end{array}}\right\}$

‎В самом деле:

‎для двупирамидной группы (91): $\sigma ^{m}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

‎для тетраэдрической группы (92): $\tau ^{2}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

‎для октаэдрической группы (93): $\sigma ^{4}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}},$

‎для икосаэдрической группы (94): $\sigma ^{5}={\begin{pmatrix}-1,&0\\0,&-1\end{pmatrix}}.$

Следовательно, порядок всех пяти групп действительно вдвое выше порядка соответствующих им групп неоднородных линейных подстановок.

---

Сноски

1. Случай $\lambda =\lambda _{1}=\lambda _{2}=3$ взят лишь для упрощения чертежа. Рассуждения, приведенные в тексте, относятся ко всякой сети четырехугольников.
2. Срав. Poincaré. Théorie des groupes fuchsiennes. Acta Mathem. Том I.
3. В этом мы убеждаемся совершенно такими же рассуждениями, которые приведены выше.
4. Основными подстановками называются такие подстановки, из которых можно составить любую подстановку группы и которые в то же время независимы между собой.
5. Подробности о циклических группах можно найти у Клейна: Vorlesungen über die Theorie der elliptischen Modulfunctionen. Стр. 186.
6. См. глава III, таблица (73).
7. По техническим причинам индексы отображаются прямым шрифтом. — Примечание редактора Викитеки.
8. См. глава III, таблица (73).
9. Мы обозначаем расстояние между точками 0 и $a$ через ${\overline {0a}}$.
10. Если $S_{0},\ S_{1},\ \ldots ,\ S_{N-1}$ суть подстановки группы и $\sigma$ есть какая-нибудь подстановка, то мы назовем группу: $\sigma S_{0}\sigma ^{-1},\ \sigma S_{1}\sigma ^{-1},\ \ldots ,\ \sigma S_{N-1}\sigma ^{-1}$
    преобразованной из первой посредством подстановки $\sigma$. Определения и свойства понятий: особая часть группы, уравнение, имеющее своей группой особую часть группы данного уравнения, и пр. излагаются в курсах высшей алгебры. См., напр., Serret. Cours d’algèbre supérieure; или: Селиванов. Теория алгебраического решения уравнений.
11. При вычислении этой подстановки необходимо знать величину отрезка ${\overline {0d}}$. Совершенно элементарным путем мы находим, что ${\overline {0d}}={\frac {1}{\sqrt {2}}}.$

12. Подстановки эти вычисляются теми же приемами, как и в рассмотренных выше случаях. Вычисления никаких затруднений не представляют.
13. При вычислении подстановки ${\mathfrak {T}}'_{\text{о}}$ необходимо заметить, что точка $d$ на чертеже 30 занимает то же положение, как и точка $d$ на чертеже 28: ${\overline {0d}}={\frac {1}{\sqrt {2}}}.$

14. Не лишено интереса замечание, что тетраэдрическая подстановка ${\mathfrak {T}}'_{\text{т}}$ есть квадрат октаэдрической ${\mathfrak {T}}'_{\text{о}}$: ${\mathfrak {T}}'_{\text{т}}={\mathfrak {T}}_{\text{о}}^{'\,2}.$

15. В конце сочинения.
16. В конце сочинения.
17. Выше, в § 1, мы определили понятие о группе каких бы то ни было операций.
18. Holoedrisch isomorph по терминологии немецких математиков.
19. Всякую группу $G$ неоднородных линейных подстановок можно преобразовать в нормальную группу того же типа.
    ‎В самом деле, построим сеть, соответствующую группе $G$ и нормальную сеть того же типа. Эти сети, как мы знаем, эквивалентны между собой. Пусть подстановка, преобразующая первую сеть во вторую, есть $\Sigma$. Преобразуя группу $G$ подстановкой $\Sigma$, мы получаем нормальную группу, соответствующую взятой нами нормальной сети.
20. Vorlesungen über das Ikosaeder. Стр. 46.