ЭСБЕ/Электрохимия

Электрохимия
Энциклопедический словарь Брокгауза и Ефрона

Словник: Электровозбудительная сила — Эрготинъ. Источник: т. XLa (1904): Электровозбудительная сила — Эрготин, с. 596—618 ( скан ) • Даты российских событий указаны по юлианскому календарю.

Электрохимия. Содержание.

Введение. Историческая справка. — Обозначения, принятые в Э. — Основные законы и принципы. — Перенос ионов. — Электропроводность растворов. — Электровозбудительная сила. — Переход химической энергии в электрическую. — Классификация гальванических элементов. — Электролиз. — Современные электрохимические теории.

Предмет Э. составляет изучение явлений, сопровождающих непосредственный переход химической энергии в электрическую и электрической в химическую. Химическая энергия среди других форм энергии играет роль собирателя богатства природы. В этой форме накоплены громадные запасы энергии; каменный уголь, торф, нефть, дерево и т. п. так называемое топливо, с одной стороны, и кислород воздуха, с другой. Непосредственный переход химической энергии топлива в другие формы энергии, кроме тепловой, совершается только при исключительных, труднодоступных условиях. В противоположность тому электрическая энергия в высшей степени удобна для использования. Электрическая энергия переходит сравнительно легко в другие формы энергии. Она является благодетелем, который везде и всюду, где появляется, оказывает неоценимые услуги человечеству. Становится теперь очевидным громадный теоретический и практический интерес, сосредоточенный на вопросе перехода химической энергии в электрическую, как на вопросе о рациональному использования богатств природы. В настоящий момент переход этот достигается сложным, окольным путем. Сначала сжигают топливо, т. е. переводят его химическую энергию в тепловую, в паровой машине тепловую энергию переводят в механическую и, наконец, в динамо-машине механическую энергию переводят в электрическую. При этом сложном пути теряется от 85 % до 90 % первоначальной химической энергии и, в лучшем случае, только 15 % её удается перевести в электрическую. Возможен ли в настоящее время иной путь? Возможно ли непосредственно в своеобразном гальваническом элементе из энергии топлива получить электрическую энергию? Современное положение этого вопроса выясняет отдел Э., трактующий о переходе химической энергии в электрическую. К этому же отделу относится общее изучение гальванических первичных элементов. Учение об этих элементах теснейшим образом связано с вопросом о переходе химической энергии топлива в электрическую. Теоретическая сторона этого учения выяснила общий вопрос: в каком случае химическое превращение может служить для получения гальванического тока. Неприменимость же в фабрично-заводской практике известных теперь гальванических элементов объясняется как раз тем обстоятельством, что они составляют также звено в цепи химическая энергия топлива — электрическая энергия. Ведь все материалы гальванических элементов получаются применением того же топлива: цинк элемента Даниеля, Бунзена, Грене, Лекланше и т. д. из своих окислов восстанавливается тем же углем, кислоты и т. п. материалы гальванических элементов получаются при участии того же топлива. Приблизительный подсчет показывает, что стоимость электрической энергии, добываемой гальваническими элементами, в среднем в сто раз превосходит стоимость той же энергии, добываемой динамо-машиной. Можно сказать, что путь от химической энергии к электрической, ведущий через динамо-машину, теперь еще выгоднее и короче пути, ведущего через гальванические элементы. Решение вопроса об элементе, в котором уголь или какое-либо иное топливо служило источником энергии, как это будет выяснено ниже, находится еще только в зачаточном состоянии; общий вопрос о практически выгодном гальваническом элементе не решен. Таким образом, в этом отделе электрохимии открыто широкое поле для будущих изобретений и открытий, и знакомство с теоретической Э. предохранит искателя в этой области от заведомо ложных щагов. Не меньший горизонт для исследователя и изобретателя открывается во второй области Э., т. е. в отделе её, трактующем о переходе электрической энергии в химическую. Здесь создаются не только совершенно новые производства продуктов, раньше с трудом добывавшихся в небольших количествах в лабораториях, как, например, производство карбидов, но и многие старые химические производства преобразуются в электрохимические. Достаточно упомянуть, что мировое производство алюминия химическим путем в 1885 г. равнялось 15 тоннам, современное же электрохимическое 1900 года составляет 6000 тонн. Химическое производство могло понизить цену алюминия до 20 франков за килогр., т. е. цена его была приблизительно в пятнадцать раз дороже меди, электрохимическое производство понизило стоимость алюминия до 3 франков за килограмм, т. е., хотя по весу алюминий и дороже меди, но объем алюминия одинаковый объему меди стоит теперь дешевле. Необыкновенная чистота осаждаемых током металлов, значительно повышающая их цену, развила особую промышленность: рафинирование металлов, т. е. их очистку путем электролиза. В 1901 г. в Америке было рафинировано 314000 тонн меди и в Европе 172000 тонн. Легкость регулировки производства, связанная с компактностью электрохимических приборов, играет также большую роль при переходе от химических производств к электрохимическим. Получение водорода и кислорода для горнов, получение веществ для беления тканей, воска и др. разработано в такой форме производства, что в любой момент, замыкая ток, можно получить количество, необходимое для данных целей. Для всей этой области электрохимии имеет решающее значение дешевый источник электрической энергии. Стремятся заменить получение электрической энергии из топлива иными источниками энергии. Их нашли в применении гидравлических сил природы: водопадов, рек и т. п.; их должно искать в утилизации других сил: силы ветра, силы приливов и отливов, даже, быть может, в силе современных наводнений. Электрохимические производства во многих случаях настолько выгодны, что, за отсутствием более дешевых источников энергии, пользуются все тем же окольным путем добывания её из топлива. Так, в Англии и Германии в 1900 г. около 60 % всей энергии, тратившейся в электрохимических производствах, добывалось из топлива. Своеобразное место в электрохимии занимают аккумуляторы, т. е. приборы, служащие для накопления химической энергии в такой форме, которая непосредственно переходила бы в электрическую энергию. Технические задачи при устройстве этих приборов имеют решающее значение. Теория их сводится к теории гальванического элемента при разряде аккумулятора и к теории электролиза при заряжении аккумулятора (см. Аккумуляторы).

Историческая справка. Первые проявления электрической энергии были открыты и наблюдались в виде действия статического электричества. Характерным отличием явлений статического электричества должно считать ничтожное количество электричества, участвующее в явлении, при громадном его напряжении. Химическое же превращение, чтобы стать заметным, требует, как раз наоборот, очень больших количеств электричества и незначительных напряжение. Оствальд в монографии «Elektrochemie, ihre Geschichte und Lehre» пишет: «Те ничтожные количества электричества, которые давали прежние несовершенные машины, были недостаточны, чтобы вызвать какие-либо бросающиеся в глаза (химические) явления. Мы видим, что физики столетия пройзводят всевозможные электрические эксперименты, меж тем химические явления, их сопровождающие, остаются незамеченными». Первые точные указания об изменении химического состава вещества при электрическом разряде принадлежат, по-видимому, Петру Бекария. Он заметил выделение меди при прохождении искры между кусками окиси меди. Эти наблюдения должны быть отнесены к середине XVIII в. Вслед затем Ван-Марум произвел целый ряд исследований над окислением металлов как в воздухе, так и в воде при действии электрической искры. В 1789 г. Ван-Труствик и Дейман потоком искр разложили воду. Характерное свойство электрической искры составляет значительно повышенная температура. Эта высокая температура вызывает при прохождении искры целый ряд химических превращений, совершающихся помимо каких-либо электрических сил, одним только повышением температуры, как напр., соединение водорода с кислородом и т. п. Такие превращения не составляют предмета изучения электрохимии. Однако существует ряд превращений, стоящих как бы на границе чисто теплового действия электрической искры и электролитического её действия. Для этих превращений мы не можем с уверенностью сказать, чтобы они вызывались одним термическим действием искры и чтобы при этом искра не играла специфической роли катализатора, т. е. ускорителя превращения. Такие превращения обыкновенно не совершаются только при повышении температуры в тех же размерах, что и при действии электрической искры. Одно из таких превращений сделалось популярным в последнее время. Открытое Пристлеем приблизительно около 1775 г., оно вскоре было подробно изучено Кавендишем. Кавендиш, пропуская продолжительное время (около месяца) поток искр через воздух, собранный над едким кали, доказал образование азотной и азотистой кислоты из воздуха. Это превращение не привлекало внимания исследователей со времени Кавендиша чуть ли не до наших дней. В самое последнее время оно сделалось предметом многих исследований и послужило темой многих патентов. Особенно выдвинулся вопрос о горении азота, т. е. соединении его с кислородом воздуха после опубликования работ лорда Рэлэ и Рамзая над выделением аргона из воздуха предварительным сжиганием азота воздуха потоком электрических искр. В 1902 г. образовалось в Америке общество (The atmospheric products Сº) с основным капиталом в миллион долларов, устроившее завод для получения горением атмосферных газов азотной кислоты. Завод этого общества находится в знаменитом районе электрохимических заводов, приводимых в действие силой Ниагарского водопада. История Э., составляющей главную часть современной Э., т. е. получение и действие гальванического тока началась, очевидно, с 1799 г., т. е. с того года, когда Вольта открыл свой вольтов столб — первую гальваническую батарею. Уже весной 1800 года Карлейль и Никольсон заметили выделение газов при прохождении гальванического тока через каплю воды. В сентябре 1800 г. Рихтер собрал уже отдельно кислород и водород. В том же году Дэви начал ряд своих знаменитых работ в области Э. Он изгнал из химии фантастическое предположение о том, что будто электричество превращает воду в кислоты и щелочи, и показал, что кислоты и щелочи, образующиеся при электролизе воды, — продукт примесей, загрязняющих в ничтожном количестве перегнанную воду. Примеси эти попадают в перегнанную воду, главным образом, благодаря незначительной растворимости стекла. Дэви доказал правоту своего взгляда, произведя электролиз в золотом сосуде. Дэви же принадлежит разложение электролизом расплавленного едкого кали и натра, т. е. выделение новых металлов калия и натрия из веществ, считавшихся до него простыми телами. Обобщив действие гальванического тока на химические соединения, Дэви дал первую электрохимическую теорию. Его теория представляет полное отождествление химических и электрических сил. Она связана логически с теорией контакта Вольты, согласно которой одного прикосновения разнородных веществ достаточно, чтобы вызвать на них противоположный электрический заряд. «Почему же не может быть» — пишет Дэви — «что электричество и сродство представляют одно и то же»… (цитировано по Каблукову). Итак, по Дэви, при соприкосновении частиц разнородных веществ они заряжаются противоположными электричествами и потом соответственно взаимно притягиваются, образуя таким образом химическое соединение. Открытое Дэви разложение считавшихся до него простых тел, произвело значительное впечатление на умы современников и весь период деятельности Дэви можно характеризовать как период выяснения вопроса: какие же вещества должно считать простым телом и какие сложным. «До работ о Дэви», — пишет Каблуков, — «едкие щелочи считались элементами, а хлор — сложным телом; после него щелочи оказались сложными телами, а хлор — элементом». Электрохимическая теория Дэви вскоре была вытеснена теорией Берцелиуса. По теории Берцелиуса все сложные вещества построены из двух частей; каждая из этих частей заранее обладает двумя электрическими полюсами. Сила полюсов у одного и того же атома или группы атомов не одна и та же, y металлов преобладают положительные полюсы, у металлоидов — отрицательные и т. п. Химическое соединение происходит взаимодействием сильнейших полюсов, скажем, при образовании повареной соли положительный полюс натрия взаимодействует с отрицательным хлора. Теория Берцелиуса оказала громадные услуги: современниками она дала толчок к систематическому изучению химических соединений и легла в основу их классификации. Эта теория обладала одним существенным недостатком: в ней еще смешивались два понятия — количество электричества и электрическое напряжение, и поэтому она пала под ударами открытий Фарадея. Она сделалась жертвой того закона Фарадея, который лег в основу современных электрохимических теорий. По теории Берцелиуса сила электрохимического сродства определялась количеством электричества на каждом полюсе, отделяющимся при электролизе группы атомов (ионе). Закон же Фарадея состоял именно в том, что одно и то же количество электричества нужно для разложения эквивалентных количеств разных химических соединений, т. е. для разделения их ионов. Берцелиус не мог примирить своей теории с законом Фарадея, оказавшимся одним из наиболее точных законов современной физики и химии. В настоящее время, конечно, мы ясно себе представляем, что хотя и одно и то же количество электричества нужно для разложения эквивалентных количеств любых веществ, но не одна и та же электродвижущая сила, а так как энергия измеряется произведением из количества электричества на электродвижущую силу, то и не одно и то же количество энергии. Фарадею мы обязаны и правильной, т. е. принятой в настоящее время, интерпретацией явлений, наблюдаемых в гальваническом элементе. Начиная с Вольты и чуть ли не до наших дней, по крайней мере до начала восьмидесятых годов, шел непрерывный спор о месте образования электричества в гальваническом элементе. Приверженцы классической теории контакта, принадлежащей самому Вольте, местом разделения положительного и отрицательного электричеств считали место соприкосновения металлов. Противники признавали, что разделение электричеств происходит там, где совершается химическое превращение. Фарадей был приверженцем химических толкований и, возражая приверженцам контактной теории, писал: «Это было бы по истине сотворением силы из ничего, подобного чему нет в природе». Этой фразой можно закончить историю развития учения о гальваническом элементе. Она была написана до формулировки закона сохранения энергии. Дальнейшее в учении о гальваническом элементе связано непосредственно с законом сохранения энергии и изложено ниже. Должно прибавить, что новейшие теории ясно рисуют картину происхождения гальванического тока, но самым существенным успехом должно считать: умение рассчитать соотношения между химической энергией и электрической. Вот это обстоятельство как бы предвидел Фарадей, писавший в 1838 году: «со временем мы будем в состоянии сравнить такие силы в телах, как тяжесть, сцепление, электричество, химическое сродство, и тем или иным способом выводить их относительные эквиваленты из их действий, теперь же мы этого не можем» (перевод Каблукова).

Обозначения, принятые в электрохимии. Для удобства дальнейшего изложения необходимо указать на обозначения величин, принятые в Э. Обозначения эти выработаны немецким электрохимическим обществом (Bunsen Gesellschaft) и доложены V-му международному съезду по прикладной химии в 1903 г. в Берлине.

p, P	Обыкновенное и осмотическое давление
v	Объем
Θ	Температура по Цельзию
Т	Абсолютная температура Т = 273 + Θ
t	Время
Q	Количество теплоты
κ	Удельная электропроводность
η	Концентрация грамм-эквивалент в кубическом сантиметре
Λ	Эквивалент. электропроводность Λ = κη
Λ∞	Та же величина при бесконечном разбавлении
α	Степень электролитической диссоциации Сохраняем здесь прежнее обозначение Аррениуса вместо γ — новое обозначение
Е	Электродвижущая сила в вольтах
W	Сопротивление в омах
J	Сила тока в амперах
ε	Потенциал выделения, отдельный потенциал
εh	Потенциал выделения по отношению к водородному электроду
εc	Потенциал по отношению к каломельному электроду
А	Механический эквивалент теплоты, равный 41,98.106 эрг для грамм-калорий при 15° (41,8.106 по новейшим определениям)
F	Электрический заряд — эквивалент 96540 кулон (новейшие измерения дают 96580).

Основные законы и принципы. Электрохимия составляет часть физической химии, сравнительно молодой дисциплины, лежащей на границе физики и химии. Очевидно, основные законы и принципы электрохимии заимствованы, главным образом, от старших её дисциплин — физики и химии. Некоторые основные законы разрабатывались в последнее время исключительно в связи с электрохимическими задачами и имеют такое доминирующее значение для электрохимии, что о них должно быть здесь упомянуто. Первенствующий закон в электрохимии — это закон Фарадея; вкратце его можно формулировать: число разложенных током грамм-эквивалентов пропорционально количеству прошедшего электричества, причем фактор пропорциональности один для всех веществ. Под числом грамм-эквивалентов подразумевается вес выделившегося вещества, деленный на его эквивалент (см. Электрохимич. эквивалент). Очевидно, что при определении весовых количеств веществ, выделяемых на электродах при прохождении одного кулона электричества, должны получиться величины, пропорциональный эквивалентному весу данного вещества. Особенно тщательно определены количества серебра, выделяющиеся при разложении растворов азотнокислого серебра. Эти определения сделаны выдающимися исследователями и дали следующие результаты:

Маскар	1,1156	миллиграммов
Лорд Рэлэ	1,1179	»миллиграммов
Ф. и В. Кольрауш	1,1183	»миллиграммов
Потье и Пела	1,1192	»миллиграммов
Рихардс (1901 г.)	1,1172	»миллиграммов
Рихардс и Гемрод (1902 г.)	1,1175	»миллиграммов

До определения Рихардса общепринято было, что кулон электричества выделяет 0,001118 г серебра, число, близкое к среднему из определений Рэлэ и Кольраушей. Очевидно, что количество электричества, нужное для выделения грамм-эквивалента серебра, т. е. 107,93 г, а следовательно, по закону Фарадея, и любого иного грамм-эквивалента, получится делением 107,93 на 0,001118. Это число обозначают F и до появления исследований Рихардса было общепризнанно его считать равным 107,93:0,001118, т. е. 96540. Новейшие исследования Рихардса и его учеников внесли небольшую поправку. Они были произведены с вольтметром (фиг. 1), в котором была введена диафрагма (а, фиг. 1) из пористой глины, защищавшая катод (с), платиновый тигель, от скорой диффузии к нему продуктов, образующихся в ничтожном количестве у серебряной палочки анода (b). Фиг. 1. Серебряный вольтаметр по Рихардсу (поперечный разрез) Раствором служит по-прежнему 15 % азотнокислое серебро. При этих условиях Рихардс окончательно установил вышеприведенное число 1,1175 мг и F = 96580. Число F, т. е. 96540 или 96580, смотря по тому, сохранить ли прежнее значение F или отдать преимущество новым определениям Рихардса, и будет характерным фактором пропорциональности закона Фарадея. Если через H обозначим эквивалентный вес и через n количество прошедшего электричества, через х весовое количество разложенного током вещества, тогда закон Фарадея можно выразить ${\frac {Fx}{H}}=n$, при постоянстве гальванического тока $n=Jt$ (см. обозначения) и, следовательно, ${\frac {x}{H}}={\frac {Jt}{F}}$. В электрохимии часто применяются первый и второй принцип термодинамики. Согласно первому принципу, т. е. принципу постоянства и эквивалентности энергий, электрическая энергия измеряется произведением количества электричества на разницу потенциалов, т. е. на величину электродвижущей силы, и равна $EJt$ (см. обозначения) джоулей. Эквивалентность электрической и тепловой энергии определяется тем, что калория равна 4,18 джоулей, джоуль же 0,239 калории (мы принимаем за вероятное число для механического эквивалента теплоты 418·10⁷ эрг или 42600 грамм-сантиметров). Очевидно, количество теплоты, выделяемое током в $t$ секунд, равно 0,2392 $EJt$ калорий. В электрохимии часто применяются законы Ома, Кирхгофа, Джоуля и др.; они изложены в статьях, трактующих об Электричестве и Гальванизме. Пользуясь обозначениями принятыми в электрохимии, закон Ома пишется $J={\frac {E}{W}}$; закон Джоуля для количества теплоты, выделяемой током в секунду $Q=0,239J^{2}W$ калорий.

Прохождение тока через растворы электролитов. Явления, изучаемые в этом отделе, как по теоретическим причинам, так и по внешним признакам не могут быть отнесены только к случаям перехода электрической энергии в химическую. Возможно наблюдать прохождение очень слабых токов помимо разложения вещества током; при этом электрическая энергия будет переходить только в тепловую энергию (см. Электролиз). В самом же общем случае, изучение явлений при прохождении тока через растворы и сплавы электролитов (те же растворы только при высокой температуре) распадается на три части: во-первых, на изучение изменения концентраций растворенных веществ у электродов, т. е. изучение явления переноса ионов, во-вторых, на изучение электропроводности растворов и, в-третьих, на изучение продуктов, выделяющихся у электродов (электролиз). Современная теоретическая электрохимия не только качественно разъясняет происходящие явления, но и устанавливает количественные зависимости между величинами, наблюдаемыми при описанных явлениях. Выше приведенные законы (Фарадея, Ома и Джоуля) и принципы (сохранение энергии) служат основанием при нахождении большинства количественных зависимостей.

Перенос ионов. Рассмотрим случай, когда при прохождения тока часть растворенного электролита разлагается, и предположим для простоты, что разложившиеся части нацело выделяются из раствора. Опыты показали, что это разложение происходит отнюдь не равномерно во всем растворе. Все изменения раствора однородного вещества начинаются у обоих электродов и, по мере прохождения тока, распространяются от электродов к средним частям раствора. Средние же части раствора остаются совершенно не измененными, если, конечно, предохранить раствор от механического перемешивания выделяющимися у электродов газами или падением внутри раствора отделившихся от катода кусочков металла или какими-либо другими факторами. Опыт показала также, что изменение концентрации при разложении, скажем, ста частей какого-либо вещества отнюдь не совершается так, чтобы половина, т. е. 50 % его исчезло у одного электрода, а другие 50 % исчезли у другого. При электролизе разбавленного раствора йодистоводородной кислоты, из ста частей разложившегося йодистого водорода 17 % исчезают у катода и 83 % у анода; водород, конечно, выделится нацело у катода, а йод у анода. Попытки выяснить механизм выделения анионов и катионов у разных электродов нужно отнести еще к 1805 г. Гротгус (уроженец теперешних прибалтийских губерний) объяснил это явление, предположив, что при прохождения тока в растворе все молекулы располагаются так, что положительные их части, катионы по Фарадею, обращены к отрицательному полюсу, а отрицательные, анионы, к положительному и что при прохождении тока происходит обмен положительных ионов с ближайшими отрицательными; благодаря этому, у положительного электрода выделяется отрицательная часть молекулы, а у отрицательного положительная. Эта теория была усовершенствована маститым Гитторфом^[1] и доведена до современного её состояния 1853—1859 года. Гитторф разъяснял, что при таком двойном обмене должно происходить движение ионов — перенос ионов, причем анионы движутся к аноду, а катионы к катоду. Он же указал, что нет надобности считать, что оба вида ионов движутся с одинаковой скоростью для того, чтобы сохранилось неизмененное состояние раствора в неприлегающих к электродам слоях — в среднем слое у (см. фиг. 3). Фиг. 2-я представляет знаменитую молекулярную схему, предложенную Гитторфом. Фиг. 2. Схема Гитторфа для явления переноса ионов Верхний двойной ряд кружков изображает состояние растворенных молекул до начала прохождения тока, нижний, — когда шесть молекул разложилось. Ясно, что число разложенных молекул по правую и левую сторону линии $xy$ не одинаково, потому что белые кружки — ионы двигались в два раза скорее черных. Вернемся для фиксации понятий на частном примере к йодистому водороду. Легко показать, что приносимые током к электродам йод и водород, концентрации йодистого водорода менять не будут, так как нацело выделятся у электродов; будут же уменьшать концентрацию только уходящие от электрода ионы (см. фиг. 2), ибо благодаря их уходу и будет происходить разложение. Следовательно, уменьшение концентрации у каждого электрода будет происходить в зависимости от скорости уходящего от электрода иона. Если общее количество разложенного током вещества обозначим через $m$ и через $a$ количество вещества, исчезнувшего у анода, тогда ${\frac {a}{m}}=n$ будет число, пропорциональное скорости переноса катиона $(U)$. У катода исчезнет $m-a$ вещества и ${\frac {m-a}{m}}=1-{\frac {a}{m}}$ будет число пропорциональное скорости переноса аниона $V$. В случае йодисто-водородной кислоты, согласно выше приведенным данным для H^· катиона, $n$ равно 0,83, а для J′ аниона $1-n$ равно 0,17. При обыкновенных опытах трудно подобрать условия, подобные электролизу йодистоводородной кислоты между угольными или платиновыми электродами, когда и водород, и йод не действуют на электроды. Обыкновенно изучают разложение солей между электродами из металлов, входящих в состав изучаемой соли, например раствор азотнокислого серебра между серебряными электродами, тогда катион выделяется нацело, а анион соединяется с металлом электрода и, след., образует снова соль, первоначально находившуюся в растворе. Очевидно, что количество соли, вновь образовавшейся у анода, будет эквивалентно прошедшему количеству электричества, т. е. то же количество $m$. Вместо уменьшения концентрация на $m-a$ у анода произойдет увеличение концентрации на $a$ (из $m$ нужно вычесть $m-a$). Очевидно, для определения относительных чисел переносов ионов $n={\frac {a}{m}}$ и $1-n={\frac {m-a}{m}}$ необходимо в этих опытах отдельно определить т. Для этой цели в цепь включают серебряный вольтметр и им определяют количество прошедшего электричества; тогда легко по закону Фарадея вычислить т. Гитторф в своих исследованиях 1853—1859 года различными методами определяет величины $n$ и $1-n$. Эти исследования легли краеугольным камнем современной электрохимии; в свое же время, отрицательное отношение самых выдающихся ученых (Магнуса, Г. Виддемана и др.), заставило автора написать следующие слова. «В моих электролитических сообщениях я взял на себя смелость критиковать и отчасти опровергать теории исследователей, высокие заслуги которых я признаю не менее их горячих приверженцев. Я никогда бы себе не позволил этой оппозиции и мои личные воззрения подчинил бы им, если бы не голые факты… Сомнение в верности этих фактов (открытый Гитторфом перенос ионов) я пытаюсь устранить тем соображением, что даже малоопытный исследователь мог бы скоро и легко доказать неверность их, и тем, что это доказательство повредило бы только мне, а не науке. Иначе обстоит дело с теориями ваших авторитетов. Как они благодетельны, если только основательны, так точно целые века разрушительно задерживают прогресс знания, если они не верны». Методы, предложенные Гитторфом для исследования относительной скорости переноса ионов весьма разнообразны. В настоящее время часто в лабораторной практике применяется метод, предложенный Нернстом и Лёбом и усовершенствованный мной. Этот метод основан на осторожном последовательном собирании после электролиза через каучуковый запор $o$ (фиг. 3) сначала нижнего анодного тяжелого слоя — $z$, потом среднего — $y$, который должен остаться неизмененным электролизом, и в конце верхнего, катодного — $x$, который становится удельно легким благодаря уменьшению концентрации соли. Фиг. 3. Прибор Кистяковского для определения переноса ионов. Обстановка опыта видна из фиг. 3, изображающей сосуд, в котором происходит электролиз хотя бы азотносеребряной соли между серебряными электродами. Углубление r предохраняет раствор от перемешивания его отпадающими от катода кусочками серебра, выделяющегося в виде дендритов. Гарантией удачи опыта является неизменяемость среднего слоя — у.

Электропроводность растворов. Уже Гитторф высказал, что изучение электропроводности может пролить свет на явления, совершающиеся в растворе при прохождении тока. Вскоре это предположение осуществилось, благодаря систематическим исследованиям Кольраушем электропроводности и открытию закона Кольрауша-Гитторфа. С современной точки зрения, электролиты проводят ток только одновременно с молекулярными перемещениями свободных ионов. «Молекулярными» написано для того, чтобы не представлять перенос ионов, как проскок от одного электрода к другому. Явление совершается подобно диффузии одного газа в атмосферу другого газа, т. е. небольшими отрезками пути, но зато одновременно всеми ионами. Для сравнения электропроводности различных растворителей принято определять удельную электропроводность, т. е. вычисляют электропроводность кубического сантиметра любого раствора, помещенного в сосуд кубической формы, причем электродами служат противоположные стенки кубика, равные, очевидно, квадратному сантиметру. Электропроводность выражают в обратных омах, т. е. за единицу электропроводности принимают тот же ом (столб ртути длины 1,063 метра, поперечное сечение 1 кв. мм). Чтобы от сосуда произвольной формы перейти к удельной электропроводности, пользуются законом, что электропроводность сосуда с прямыми параллельными стенками уменьшается пропорционально расстоянию между электродами l и увеличивается пропорционально поперечному сечению сосуда f, если только с этим сечением совпадают по величине, форме и положению электроды. Очевидно, $\chi =W^{-1}{\frac {l}{f}}$ (см. обознач.). Чтобы измерить электропроводность предложено несколько методов: Бути, Кирхгофа, Кольрауша и др. Задача, которую должно преследовать при измерении электропроводности электролита, заключается в сохранении неизмененного состояния раствора у электродов при прохождении тока. Это достигнуто Кирхгофом и Кольраушем применением переменных токов. Метод для сравнения электропроводностей основан на мостике Уитстона (см. Гальванопроводность и электропроводность металлов). Успех метода Кольрауша должно приписать тому обстоятельству, что для определения отсутствия тока в соединительной ветви cd мостика Уитстона им был использован телефон. Когда в телефоне наблюдается минимум силы звука, тогда отношение сопротивлений R к W равно отношению ad к db, т. е $W^{-1}=R{\frac {ad}{db}}$; отсюда $\chi =R{\frac {ad}{db}}{\frac {l}{f}}$. Значение R отсчитывается в магазине сопротивления непосредственно числом введенных омов, отношение ad к db получается отсчетом на мостике. На фиг. 4 приведен случай, когда оно равно 42:58. Фиг. 4. Схема мостика Уитстона. Остается определить ${\frac {l}{f}}$ для данного сосуда. Эти определения делаются для сосудов формы, приведенной на фигуре 5 A, В и D, пользуясь величинами удельной электропроводности растворов, определенными Кольраушем в сосудах С фигуры 5. 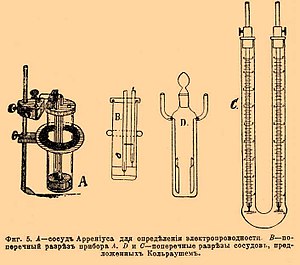Фиг. 5. A — сосуд Аррениуса для определения электропроводности; B — поперечный разрез прибора А; C и D — поперечные разрезы сосудов, предложенных Кольраушем. Перемещая электрод в сосуде С (фиг. 5) на расстояние l, зная начальную электропроводность и полученную после перемещения, а также поперечный разрез сосуда f, Кольрауш из уменьшения электропроводности, соответствовавшей введению столба жидкости длиной в l и поперечного разреза f, вычислял удельную электропроводность. Этим приемом Кольрауш обошел трудность полного совпадения электрода с поперечным разрезом сосуда. Определенные им точные величины для электропроводности целого ряда жидкостей послужили основанием для определения ${\frac {l}{f}}$, так называемой «емкости» любого сосуда. Зная κ для данной жидкости, наливая ее в любой сосуд (см. фиг. 5) и определяя R и ad/db на мостике Уитстона, вычисляют ${\frac {l}{f}}$ для нового сосуда из уравнения $\chi =R{\frac {ad}{db}}{\frac {l}{f}}$. Фигура 6 дает общую обстановку опыта определения электропроводности. Ниже приведенная таблица дает электропроводности некоторых водных растворов в обратных омах, служащие для определения емкости сосудов.

	κ при 18°	κ при 25°
Насыщенный раствор поваренной соли (NaCl)	0,21605	0,25130
Нормальный раствор хлористого калия (KCl) 74,6 грамма в литре раствора	0,09822	0,11180
110 норм. раствор KCl, т. е. 7,46 г в литре	0,01119	0,01288
150 нормальный раствор KCl 1,492 г в литре	0,002397	0,002765
1100 нормальный раствор KCl 0,746 г в литре	0,001225	0,001413

Как видно из таблицы, электролитическая электропроводность, в противоположность металлической, значительно увеличивается с повышением температуры. Поэтому следует помещать сосуды, в которых определяют электропроводность, в термостаты, т. е. в приборы, поддерживающие постоянную температуру: На практике чаще всего применяют термостаты (см. фиг. 6) с температурами 18° и 25° по Цельзию. Фиг. 6. Приборы для определения электропроводности. 1; 1 — обозначают мельницу Оствальда, вращающую соду в сосуде термостата током воздуха от горелки (1); 2 — сосуд Аррениуса для определения электропроводности (форма, суженная книзу); 3 — держалка приб.; 2; 4 — терморегулятор; 5 — термометр, 6 — магазин сопротивления; 7 — мостик; 8 — маленькую спираль Румкорфа; 9 — телефон; 10 — ключ для замыкания тока; 11 — элемент гальванический. Для вычисления небольших отклонений от температур 18° и 25° пользуются температурными коэффициентами для изменения электропроводности. При изменении температуры на 1° от 18° электропроводность повареной соли при сохранении насыщенности изменяется на 0,00492; нормального хлористого калия на 0,00192; 110 норм. на 0,00024; 150 норм. 0,000052 и 1100 норм. на 0,000026. В общем случае изменение это составляет при сохранении постоянства концентрации раствора около 2 % на градус. Из приведенной таблицы также видно, что удельная электропроводность водных растворов уменьшается с разбавлением, что является общим правилом для водных растворов крепости меньше 5 %. Электропроводность электролитов в других растворителях, как, например, в жидкой сернистой кислоте (исслед. П. И. Вальдена) не следует правильностям, найденным для водных растворов, и часто с повышением температуры уменьшается, становясь при критической темп. растворителя равной нулю. Современные теории признают, что растворы электролитов проводят ток только благодаря «Гитторфовским» переносам ионов. Так что удельная электропроводность должна быть равна абсолютному числу ионов, находящихся в кубическом сантиметре, умноженному на количество электричества, находящаяся на каждом ионе (ξ) и на величину пути, который пройдет каждый из ионов, т. е. $U+V$. Отсюда $\kappa =N_{1}\xi (U+V)$, где $N_{1}$ — абсолютное число электролитически диссоциированных эквивалентов растворенного электролита. Величина ξ порядка 10^—19, величина $N_{1}$ меняется с концентрацией раствора, однако она порядка от 10¹⁵ до 10²⁴. Обе эти величины трудно поддаются точному измерению, поэтому произведение $N_{1}\xi$, дóлжно заменить более доступными для измерения величинами. Обозначим через $N_{2}$ абсолютное число молекул, находящихся в грамм-молекуле одноэквивалентного вещества, или абсолютное число эквивалентов многоэквивалентного электролита. Тогда $N_{2}\xi$ будет количество электричества на грамм-эквиваленте, т. е. F. Отсюда $\xi ={\frac {F}{N}}$. Величина ${\frac {N_{1}}{N_{2}}}$, т. е. отношением абсолютного числа эквивалентов, находящихся в кубическом сантиметре, ко всему абсолютному числу эквивалентов в грамм-эквиваленте вещества ($N_{2}$), соответствовала бы эквивалентной концентрации η, если бы все молекулы вещества проводили ток. По теории Аррениуса (см. Электрол. диссоциация), α составляет долю проводящих молекул. Следовательно, ${\frac {N_{1}}{N_{2}}}=\alpha \eta$. Подставляя вместо $N_{1}$ и ξ соответствующие величины, получаем, что $\kappa =\alpha \eta F(U+V)$, или, подставляя вместо $UF=u$ и $VF=v$ и ${\frac {\kappa }{\eta }}=\Lambda$ (см. обозначения), получаем $\Lambda =\alpha (u+v)$. Эта Λ представляет весьма характерную величину для растворов, так назыв. эквивалентную электропроводность. Её значение обыкновенно увеличивается с разбавлением и достигает для очень разбавленных растворов наибольшей постоянной величины, обозначаемой $\Lambda \infty$. Принимая, что в правой части равенства все величины, кроме α, постоянны (это можно с большей вероятноотью считать для не очень крепких растворов), получаем, что единственная величина, которая увеличивается с разбавлением, это степень электролитической диссоциации, т. е. α. Очевидно, что для самых разбавленных растворов, когда все ионы участвуют в переносе, α делается равной единице и тогда формула пишется

$\Lambda \infty =u+v$.

Эта формула имеет важное значение в современной электрохимии; сравнение её с $\Lambda =\alpha (u+v)$ дает возможность теоретически обосновать способ вычисления а из отношения $\alpha ={\frac {\Lambda }{\Lambda \infty }}$. Точность такого вычисления α в настоящее время оспаривается Яном и Нернстом. Они указывают, что величины U и V, т. е. абсолютные скорости переноса ионов, не остаются постоянными для растворов любых концентраций. Однако возможность приблизительного вычисления величины α таким путем ни Ян, ни Нернст не отрицают. Второе следствие формулы $\Lambda \infty =u+v$ еще важнее; это закон Кольрауша-Гитторфа. Очевидно, что величины и и v, носящие название подвижности ионов, могут быть вычислены из максимальной эквивалентной электропроводности делением её на части, пропорциональные Гитторфовским числам переноса ионов. Полученные таким путем величины подвижности должны быть постоянной величиной для данного иона независимо от того электролита, из электропроводности которого ее вычислить, потому что ионы при переносе не оказывают влияния друг на друга. Обратно — сумма этих подвижностей должна дать максимальную электропроводность любого электролита, что и составляет закон Кольрауша-Гитторфа. Приведем данные для подвижностей ионов при 18° из определений Кольрауша и Гольборна:

Ион калия К·	65,3
»Ион натрия Na·	44,4
»Ион лития Li·	35,5
»Ион аммония NH4·	64,2
»Ион серебра Ag·	55,7
»Ион бария 12 Ва··	57,3
»Ион стронция 12 Sr··	54,0
»Ион кальция 12 Са··	53,0
»Ион магния 12 Mg··	49,0
»Ион цинка 12 Zn··	47,5
»Ион водорода H·	318
»Ион хлора Cl′	65,9
»Ион йода J′	66,7
»Ион остатка азотной кислоты NO3′	60,8
»Ион»остатка хлорноватой кисл. ClO3′	56,2
»Ион»остатка уксусной кисл. С2Н3О2′	33,7
»Ион»остатка серной кисл. 12 SO4″	69,7
»Ион»остатка щавелевой кисл. 12 C2O4″	63
»Ион гидроксила ОН′	174

Коэффициент 12 обозначает, что вычисляемая из подвижности ионов электропроводность относится к случаю раствора грамм-эквивалента соли двухэквивалентного иона. Применяя закон Кольрауша-Гитторфа, вычисляем максимальную электропроводность для хлористого калия KCl, равную 65,3 + 65,9 = 130,2; для едкого барита ½ Ва(НО)₂ = 231,3; для соляной кислоты HCl 318 + 65,9 = 383,9 и т. д. Из просмотра этих данных видно, что максимальные эквивалентные электропроводности всех солей величины сравнительно близкие, для щелочей величины большие чем для солей приблизительно на 100 и для кислот на 250. Чтобы из вышеприведенной таблицы вычислить эквивалентную электропроводность для любой концентрации соли, нужно сумму подвижностей её ионов умножить на степень электролитической диссоциации α. Для вычисления κ, т. е. удельной электропроводности, полученные величины от умножения на α умножить на η, т. е. на число грамм-эквивалентов соли, растворенное в кубическом сантиметре. Первое время после открытая закона Кольрауша-Гитторфа его считали неприменимым к многоэквивалентным солям. Тщательные исследования расширили район действия этого закона. Причина неприменимости закона зависела от того опытного материала, которым пользовались. Уже Гитторф нашел, что только в разбавленных растворах числа переноса для солей остаются постоянными. По мере же концентрирования раствора эти числа более или менее меняются. Главная причина изменения этих чисел, как ясно уже понял Гитторф, лежит в возможности удвоения растворенных молекул, в связи с этим возможность анормальной электролитической диссоциации с образованием сложного аниона, так назыв. комплексного аниона по типу Cd₂Cl₄ = Cd^·· + CdCl₄″, открытому уже Гитторфом, или сложного катиона по типу, предсказанному мной в 1890 г. при изучении изменения чисел переноса ионов для солей серебра и открытому позднее Абеггом и Гельвигом. Исследованная ими соль AgJ(AgNO₃)₂ ионизирует, как подтвердили и мои опыты на Ag₃J^·· + 2(NO₃′). Чтобы избавиться от этих отступлений, нужно перейти к изучению переноса ионов разбавленных растворов (1 % и меньшей концентрации). В разбавленных растворах наступает распадение двойных молекул и наблюдается нормальная электролитическая диссоциация. Мной были изучены растворы таких сложных солей, как K₄Fe(CN)₆, К₃Со(CN)₆, Ag₃·Cr(C₂O₄) и, несмотря на то, что K₄Fe(CN)₆ может в крепких растворах анормально ионизировать на К^· + K₃Fe(CN)₆′ или 2К^· + K₂Fe(CN)₆″ или 3К^· + KFe(CN)₆‴ в разбавленных растворах, закон Кольрауша-Гитторфа для этих солей подтверждается, т. е., другими словами, в них наступает нормальная ионизация на 4К^· + Fe(CN)₆‴ или 3К^· + Co(CN)₆‴, а также 3Ag^· + Cr(C₂O₄)‴.

Теоретический интерес формулы $\Lambda \infty =F(U+V)$ значительно возрастает, если указать, что величины U и V, т. е. абсолютные скорости ионов или число сантиметров, на которые перемещается данный ион в секунду, возможно непосредственно наблюдать и, следовательно, сравнить с вычисленными из подвижностей вышеприведенной таблицы, так как $U={\frac {u}{F}}$ и $V={\frac {v}{F}}$. Что бы фиксировать понятия, вернемся к расчету с йодисто-водородной кислотой. Для неё $\Lambda \infty =u+v$ равна 385; из этого числа, согласно выше приведенным данным, 83 % приходится на скорость переноса иона водорода, т. е. 318; разделив эту величину на F, т. е. на 96580, получим 0,0033 см в секунду. Лодж, наслаивая раствор кислоты и щелочи, следил за тем, с какой скоростью при прохождении тока перемещалась поверхность, отделявшая бесцветную кислоту от окрашенной фенол-фталеином щелочи. При нейтрализации кислотой щелочная окраска фенолфталеина, как известно, исчезает. Измеряя скорость перемещения отделяющей оба раствора поверхности, Лодж нашел величины, близкие к вычисленным Кольраушем. Для иона водорода он нашел 0,0029 см в секунду. Такое число нужно считать сравнительно хорошим подтверждением теоретических опытов. Опыты Лоджа с кислотами представляют значительные экспериментальные трудности. Ветамм повторил опыты Лоджа, наблюдая перемещение под влиянием тока окрашенного иона двухромовокислого калия на границе углекислого калия, и нашел, что скорость перемещения границы 0,000475; вычисленная из данных Кольрауша и Гитторфа она получается 0,000473. В заключение этой главы должно еще сказать несколько слов об электропроводности смесей. Этот вопрос стоит в связи с влиянием электропроводности растворителя на электропроводность растворенного в нем вещества. В случае отсутствия химического взаимодействия принимается, что растворение малого количества нового вещества увеличивает электропроводность на свойственную веществу величину, не влияя на первоначальную электропроводность самого растворителя, если только она была малой величиной.

Электровозбудительные силы. Пока ионы движутся внутри однородного раствора, им не приходится преодолевать никаких иных сил, кроме сопротивления, оказываемого движению ионов данным раствором. Как только ион достигает границы однородности раствора или вообще границы какой-либо новой среды, явление усложняется. На этих границах иону приходится преодолевать особые силы, носящие название электродвижущих или электровозбудительных сил. Величина электродвижущей силы определяется разницей потенциалов на границах однородности. Измерение этих сил трактуется подробно в физике (см. Электрич. измер.). При электрохимических же измерениях пользуются чаще других методами, основанными на непосредственном применении закона Ома, а также некоторыми компенсационными методами, прототип которых предложен Поггендорфом. С самого начала должно заметить, что не существует приемов для измерения электродвижущей силы на одной какой-либо границе однородности. В лучшем случае для измерения приходится погружать в электролит два электрода и, следовательно, измерять разницу потенциалов на двух границах однородности. Погружают в электролит разные металлы; иначе при электродах двух одинаковых металлов и одном электролите электровозбудительные силы на границах однородности будут одинаковы и противоположны, а следовательно, взаимно друг друга уничтожать. Очевидно, что, кроме границ однородности электролит-металла, границами однородности будут также места соприкосновения разных металлов, ведущих к измерительным приборам. Все величины электровозбудительных сил на границах двух металлов принимаются равными нулю. На самом деле они представляют ничтожно малые величины, настолько малые, что при всех измерениях, идущих до тысячных долей вольта, ими можно пренебречь. Простейшие измерения электродвижущих сил основаны на применении чувствительных гальванометров и введении в цепь известных больших сопротивлений ($W_{2}$). По закону Ома Невозможно разобрать выражение (SVG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «http://localhost:6011/ru.wikisource.org/v1/»:): {\displaystyle J = \frac{E}{W_1 + W_2}} , пренебрегая величиной $W_{1}$ по сравнению с $W_{2}$ получаем $J={\frac {F}{W_{2}}}$. Величину J дает гальванометр или вольтметр. Вводя в цепь очень большое, измеренное в омах сопротивление ($W_{2}$) и серебряный вольтметр, определяют точно время прохождения тока и по формуле ${\frac {xF}{t}}={\frac {E}{W_{2}}}$, где х выражен в грамм-эквивалентах, т. е. вес осажденного током серебра, деленный на эквивалентный вес серебра (107,93), определяют Е, т. е. электродвижущую силу. Значение F и t см. обозначения. Этим приемом возможно пользоваться только при постоянстве Е во все время опыта, т. е., напр., для нормальных элементов Клерка, Гельмгольца и Уитстона (см. ниже). В электрохим. исследованиях часто применяют также компенсационный метод, схему которого представляет фиг. 7. Фиг. 7. Схема компенсационного метода определения электровозбудительной силы. А — аккумуляторы, Х — ключ для замыкания тока. ВС — проводник постоянного поперечного сечения и, следовательно, постоянного линейного сопротивления, N — так назыв. нормальный элемента (см. ниже), Е — прибор для наблюдения отсутствия тока может быть гальванометр или электрометр Липмана (см. фиг. 9), D — место подвижного контакта. Контакт перемещают до тех пор, пока в Е будет наблюдаться отсутствие тока. Очевидно, что при этом падение потенциала вдоль BD равно и противоположно величине электровозбудительной силы нормального элемента; падение же потенциала вдоль всей ВС будет во столько раз больше, во сколько ВС больше BD. Заменяя нормальный элемент измеряемой электровозбудительной силой и снова перемещая D, т. е. место контакта до прекращения тока в измерительном приборе E, определяют новое положение D₁. Измеряемая электро-возбудительная сила будет равна $N{\frac {BD'}{BD}}$, где N — электровозбудительная сила нормального элемента. Лучшим нормальным элементом должно считать элемент Клерка. Элементы эти имеются в продаже, выверенные берлинским имперским институтом. Составные части элемента Клерка: 10—15 % амальгама цинка, покрытая частью закристаллизовавшимся насыщенным раствором сернокислого цинка. Положительный полюс элемента образует ртуть, покрытая слоем сернокислой ртути, соприкасающейся с тем же раствором сернокислого цинка, насыщенным, конечно, и сернокислой ртутью. Электровозбудительная сила этого элемента

Е = 1,4328 — 0,00119 (Θ − 15) − 0,000007 (Θ − 15)² вольт.

Элемент Уитстона составлен так же, как и элемент Клерка, только цинк и цинковые соли в нем заменены кадмием и кадмиевыми солями.

Е = 1,0186 − 0,000038 (Θ − 20) вольт.

Элемент Гельмгольца состоит из цинка, раствора хлористого цинка уд. в. 1,409 при 15°, каломели и ртути. При 15° его электровозбудительная сила равна 1 вольту, а изменение с температурой составляет только + 0,00007 на один градус. При пользовании нормальными элементами только для очень слабых токов, они сохраняют постоянство электровозбудительной силы в продолжение нескольких лет.

Отдельные потенциалы. Как было сказано выше, не существует методов, дающих возможность непосредственно измерить разницу потенциалов на границе электрод и электролит. Пытались поэтому различными приемами вычислить эту разницу. На такие приемы впервые указал Гельмгольц. Один из них основан на предположении, что в известных случаях электровозбудительная сила на границе ртуть и электролит равна нулю. Такие случаи наступают, когда ртутная поверхность быстро обновляется, т. е. когда ртуть из капилляра маленькими, быстро следующими друг за другом, каплями вытекает в электролит. Причина возможности наступления отсутствия электродвижущей силы заключается в том, что каждая отрывающаяся капля ртути уносит с собой свой электролитический двойной слой (см. Электролитическая растворимость) и, следовательно, уносит часть ионов с границы ртуть-электролит. Новый двойной слой может образовываться до тех пор, пока на этой границе будет достаточно ионов ртути; когда же раствор обеднеет ими настолько, что осмотическое давление ионов ртути сделается равным упругости электролитического растворения ртути, двойного слоя образовываться больше не будет, т. е. раствор и ртуть будут обладать одинаковыми потенциалами. Другой метод основан на свойстве ртутной капли менять свою форму в зависимости от степени электризации её поверхности. Это свойство ртутной капли легко демонстрировать опытом, который носит название «Электрохимич. сердце». Каплю ртути размером сантиметр в поперечнике помещают в большое часовое стеклышко, сверх неё наливают слабого раствора серной кислоты, затем прибавляют несколько капель раствора двухромовокислого калия и прикасаются к краю ртутной капли (фиг. 8) железным острием. Фиг. 8. Опыт пульсации ртутной капли, называемый «электрохимическое сердце»: а — ртутная капля; b — железное острие Ртуть приходит в пульсирующее движение то прикасаясь к железному острию, то снова отделяясь от него. Пульсация ртути при удачно поставленном опыте длится целые часы. Объясняется она тем, что до прикосновения к железному острию поверхность ртути покрыта электролитическим двойным слоем, взаимное отталкивание наэлектризованных частиц этого слоя придает капле ртути более плоскую форму, в момент её прикосновения к железному острию образуется ток, ртуть отдает железу положительное электричество и капля её сейчас же принимает более выпуклую форму, отдаляясь от острия, затем тотчас же она снова электризуется и т. д. Подобное же влияние электризации можно наблюдать, вводя в замкнутую гальваническую цепь ртуть, наполняющую часть капилляра, остальная часть которого заполнена серной кислотой (фиг. 9). Фиг. 9. Видоизмененный Оствальдом электрометр Липмана: с — конец ртутной нити; d — раствор серной кислоты Ртуть соединяют с отрицательным полюсом батареи, серную же кислоту с положительным. При постепенном увеличении электровозбудительной силы ртуть в цилиндрическом капилляре в точке c (фиг. 9) понижается (перемещается влево). При некоторой определенной электровозбудительной силе поверхностное натяжение ртути достигает максимума и наблюдается наибольшее понижение. При дальнейшем увеличении электровозбудительной силы ртуть снова повышается в капилляре. Самое большое понижение при электролите серной кислоты и втором ртутном электроде получается, когда Е батареи равно 0,93 вольт (этим свойством ртутной нити пользуются для устройства капиллярных электрометров. Один из таких электрометров изображает фиг. 9. Применение их основано на том, что определенной электровозбудительной силе замкнутой цепи соответствует определенное положение точки с — конца ртутной нити. Если в цепи сумма посторонних электрометру электродвижущих сил равна нулю, положение с наблюдается то же, что и при замыкании электрометра на себя, т. е. при соединении двух его проводников а и b). Очевидно, что наиболее близкая к шару форма ртути или наибольшее понижение её поверхности в капилляре наступит, когда на границе ртуть и электролит будет полное отсутствие электролитического двойного слоя, уменьшающего поверхностное натяжение ртути. Пользуясь обоими выше приведенными принципами, Оствальд определил абсолютные разницы потенциалов каломельных электродов (см. Электроды), найденные им равными 0,56 вольт при наполнении нормальным раствором хлористого калия и 0,616 при наполнении ¹/₁₀ нормал. Так как хотя бы для одного электрода известна абсолютная разница потенциалов, т. е. так наз. электродный потенциал или отдельный потенциал, не представляет никакого труда, комбинируя данный электрод с другим электродом, определить величину электродного потенциала любого другого электрода. Дело при этом усложняется тем обстоятельством, что на границе электролита каломельного электрода и электролита, в который будет погружен изучаемый электрод, тоже существуют электровозбудительные силы. Однако эти затруднения легко устраняются возможностью довести величины этих электровозбудительных сил до минимума. Причина их — разница в концентрации ионов. Нернст дал теорию, которая дает возможность из концентрации ионов вычислить разницы потенциалов на границе электролитов. Главные затруднения в определении отдельных потенциалов обнаружились, как только были применены новые методы, разработанные в последнее время Биллитцером. Всякая небольшая металлическая частичка, подвешенная в электролите, окружена двойным «Гельмгольцевским» слоем, следовательно, наэлектризована. Оказывается, что, как только через раствор проходит гальванический ток, такая частица в зависимости от своей электризации движется то к аноду, то к катоду и только в случае отсутствия на ней двойного слоя, т. е. когда на границе частицы и электролита нет электровозбудительной силы, она остается в покое. Изменяя состав электролита, Биллитцер заставлял одним и тем же током частицы коллоидальных растворов платины, серебра и ртути, равно как и тонкие подвешенные металлические пластинки, перемещаться то в одну, то в другую сторону. Момент изменения направления перемещений частицы должен наступить для электролита, на границе которого электровозбудительная сила данного металла равна нулю. Исследования Оствальда позвозили предвычислить состав таких электролитов. Опыты Биллитцера не подтвердили предвычисленные по Оствальду данные. Таким образом, в настоящий момент дóлжно снова отказаться от знания абсолютных величин отдельных потенциалов и должно вернуться к предложению, сделанному Нернстом. Нернст предложил перейти к расчету с относительными величинами отдельных потенциалов, причем за отдельный потенциал, равный нулю, принять разницу потенциала на границе водород-платиновый электрод (см. Электроды) и нормальный раствор соляной кислоты. Величины таких отдельных потенциалов приведены ниже в главе, трактующей о переходе химической энергии в электрическую.

Переход химической энергии в электрическую. Отдельные загадочные для современников действия двух соприкасающихся металлов были известны с 1760 г. Зульцер сделал ряд наблюдений, согласно которым два соприкасающихся металла — «один характера свинца, другой серебра» — при одновременном прикосновении к языку вызывают вкусовые ощущения, не вызываемые каждым металлом в отдельности. Однако, только со времени Гальвани и Вольты, т. е. в последнее десятилетие XVIII века, началось систематическое изучение явлений, вызываемых соприкосновением металлов с системой жидких проводников. Теория же этих явлений, при которых, согласно современным воззрениям, совершающаяся на границе металла и электролита химические превращения служат источником гальванического тока, разработана только в самое последнее время Гельмгольцем, Нернстом и Оствальдом. Первый вопрос, который приходится решить при изучении взаимного перехода энергий, заключается в следующем: при каких условиях химическое превращение может служить источником гальванического тока? Другими словами, как заставить химическую энергию данного превращения переходить не в тепловую, как это обыкновенно наблюдается, а именно в электрическую? Ответ на этот вопрос был дан Оствальдом: нужно химическое превращение разбить на две части так, чтобы одна часть этого превращения совершалась у одного электрода, другая у другого, причем посредниками между частями этого химического превращения являются приведенные в движение ионы электролитов, находящихся между электродами. Другими словами, только в том случае химические или какие-либо иные причины (разница концентрации в концентрационных цепях) могут быть источником гальванического тока, если они вызывают движение ионов в электролите. Чтобы иллюстрировать это положение, приведем пример, указанный Оствальдом. Дана комбинация: в сосуде из пористой глины имеется цинк, к которому налит раствор цинкового купороса, снаружи раствор сернокислого калия, в которые погружена медная пластинка; схематически это изображают Zn | Zn SO₄ | K₂SO₄ | Cu. Такая комбинация не даст более или менее продолжительного гальванического тока. Спрашивается: куда дóлжно налить серную кислоту, чтобы химической реакцией растворения цинка с выделением водорода получить гальванический ток? Правильный ответ: ее нужно налить к меди (а не к цинку). При этом, если замкнуть цепь, цинк начнет, из-за своей электрохимической упругости растворения (см. соотв. статью), растворяться в цинковом купоросе, ионы цинка Zn^·· будут перемещаться к меди, а ионы SO₄″ к цинку. В направлении же к меди будут перемещаться ионы водорода Н^·. Водород отдаст положительное электричество меди и выделится у меди в газообразном состоянии. Во внешней цепи гальванический ток пойдет от меди к цинку. Химическое превращение разбито на две части; цинк растворяется у одного полюса элемента, а водород выделяется у другого. При изобретении новых гальванических элементов нужно иметь всегда в виду такое соотношение между превращением и током. Выяснено оно в самое последнее время. Наш гениальный изобретатель Яблочков пытался получить гальванический элемент, поддерживая горение угля в расплавленной селитре. Нам ясна неудача его опытов. В угольном элементе сжигающее уголь начало, т. е. источник кислорода, должен быть у второго полюса, а не у угля! Одна из причин, вызывающих движение ионов, а следовательно, могущих вызвать образование гальванического тока, это разница концентраций и состава растворов. Простейший случай будет: крепкий и слабый раствор одного и того же электролита. Движение ионов на границе таких растворов будет вызвано бóльшим осмотическим давлением концентрированного раствора, благодаря чему происходит диффузия растворенных частей в сторону падения концентрации. Такая диффузия не будет вызывать электрических явлений, если оба иона движутся с одинаковой скоростью, но если только скорость ионов не одинакова (см. таблицу подвижности ионов), тогда более быстрый ион будет обгонять медленный и будет своим зарядом электризовать разбавленный раствор. Очевидно, что степень электризации определится той силой, которая приводит в движение ионы и вызывает диффузию, т. е. осмотическим давлением. Непосредственное измерение электровозбудительной силы на границе крепкого и слабого растворов очевидно невозможно. Необходимо в растворы погрузить электроды. Расчет величины электровозбудительной силы для одного из таких случаев, для так называемого концентрационного элемента Гельмгольца, теоретически разработан самим изобретателем и подтвержден и проверен на опыте Нернстом и его учениками. Этот случай разобран ниже в главе «концентрационный элемент». Движение ионов может быть вызвано способностью электрода растворяться в виде ионов в растворе электролита (см. Электролитическая растворимость). Движения ионов не наступает, если нет вышеприведенных условий для химического превращения, т. е. разделения его на две части. В общем случае, величина электровозбудительной силы определяется величиной электролитической упругости растворения металлов и противодействием ей осмотического давления находящихся уже в электролите ионов соответствующего металла. Очевидно, следовательно, что разница потенциалов на границе метал-электролит только в том случае является определенной величиной, если указана концентрация соли данного металла в растворе. Как уже выше было сказано, абсолютные величины разницы потенциалов определенные методами Гельмгольца-Оствальда на границе электрод-электролит не представляются достаточно достоверными величинами. Теоретически они вычисляются формулой Нернста $E={\frac {RT}{nF}}\mathrm {log.nat.} {\frac {P}{p}}$, где P — упругость растворения металла, p — осмотическое давление ионов металла в растворе; n — обозначает валентность металла; величины R; Т и F см. обозначения. Для температуры 18° формула Нернста принимает вид $E=n^{-1}0,000198T\log {\frac {P}{p}}$ и для обыкновенной комнатной температуры 18° Цельсия $E=n^{-1}0,0577x\log {\frac {P}{p}}$. Коэффициенты 0,000198 и 0,0577 вычисляются из следующих данных: R — газовая константа в джоулях равна 4,18 х 1,99; F = 96580; T = 273 + 18. Для перехода от натуральных логарифмов к десятичным нужно умножить на 2,3026. Однако величины Р непосредственно не измеряются. Приведенные в статье Электролитическая растворимость величины для Р вычислены при условии признания верности метода Гельмгольца-Оствальда для определения абсолютного потенциала. Они верно дают соотношение величин Р для разных металлов, но абсолютное их значение поколеблено новейшими исследованиями Биллитцера. Поэтому ниже будут приводиться только относительные величины электродных потенциалов при принятии, согласно Нернсту, отдельного потенциала для водорода—платинового электрода в нормальной соляной кислоте равным нулю. Платиновая пластинка, служащая электродом, должна быть платинирована, притом в постоянном соприкосновении частью платинированной поверхности с газообразным водородом и предварительно насыщена водородом, что достигается электролизом. Ниже приведенные величины электродных потенциалов $\varepsilon _{h}$ показывают, какая электровозбудительная сила наблюдается в элементе, электродами для которого служат металл, электролитом нормальный (грамм-эквивалент в литре) раствор соли металла, а другим электродом является водород—платиновый электрод, погруженный в нормальный раствор соляной кислоты. Производить измерения отдельных потенциалов с водородным электродом очень сложная задача. Обыкновенно производят измерения с каломельным электродом (см. Электроды), комбинируя с ним изучаемый электрод. Разница электровозбудительной силы нормального каломельного и водородного электрода составляет −0,283 вольт. Положение предполагавшегося абсолютного нуля потенциала получится в Нернстовской шкале между талием и кобальтом, согласно расчету 0,56 − 0,283 = 0,277.

Электродные потенциалы по Нернсту.

Марганец Mn	1,075
Цинк Zn	0,770
Кадмий Cd	0,420
Железо Fe	0,340
Таллий Tl	0,320
Кобальт Со	0,230
Никель Ni	0,230
Свинец Pb	0,150
Водород Н	±0,000
Медь Cu	−0,230
Ртуть Hg	−0,750
Серебро Ag	−0,770
Палладий Pd	< −0,790
Платина Pt	< −0,860
Золото Au	< −1,080

Чтобы из данных Нернстовой шкалы получить величины абсолютных потенциалов, нужно вычесть 0,277. Для марганца получится 0,798 и для серебра — 1,047. Знак < показывает, что электровозбудительная сила для этих металлов численно должна быть больше и не могла быть определена соответствующим опытом, т. е. погружением электродов в растворы солей значительно электролитически диссоциированных, ибо таковых солей для данных металлов не имеется (см. Электролитическая диссоциация). Таблица электродных потенциалов дает нам возможность вычислить электровозбудительную силу любой комбинации и приведенных электродов. При расчете электровозбудительные силы противоположных полюсов должно взаимно вычитать. Положительные величины указывают, что данный элемент обладает большей упругостью растворения, чем водород, и, следовательно, выделяет его из кислот. Ниже приведены определения для электровозбудительных сил, вызываемых химической реакцией образования водных растворов галоидных кислот. Электродами служат, с одной стороны, тот же водород-платиновый электрод, электровозбудительная сила которого приравнивается нулю, и кислород-платиновый или галоид-платиновый электрод, погруженные в нормальный раствор кислоты.

Электродные потенциалы по Нернсту:

Cl′	−1,42
Br′	−0,99
J′	−0,52
½ O″	−1,12

Электровозбудительная сила этих элементов зависит от давления, под которым находится газ. С увеличением этого давления электровозбудительная сила возрастает. Для случаев, когда газ находится под атмосферным давлением, найдены вышеприведенные величины электродных потенциалов. Эти числа могут служить для расчета электровозбудительных сил любых возможных с данными электродами гальванических комбинаций. Наибольшую электровозбудительную силу, очевидно, возможно получить из комбинации: марганец, раствор хлористого марганца, соляная кислота и хлор-платиновый электрод Mn | MnCl₂ | HCl | Cl. Электровозбудительная сила будет равна 1,075−(−1,42), т. е. около 2,5 вольт. Прежде чем перейти от данных химических превращений, совершающихся у обратимых электродов, к более сложным необратимым, дóлжно указать на некоторые характерные свойства элемента Грове, т. е. цепи, состоящей из водород-платинового и кислород-платинового электродов. Электровозбудительная сила этого элемента мало изменяется с изменением электролита, в который погружены оба электрода. Она долгое время считалась близкой к 1,08 вольта, в самое последнее время исследования Бозе, Чепинского и др. показали, что она выше, именно около 1,12. Причина малой электровозбудительной силы лежала в ненасыщенности платиновых электродов водородом и кислородом. Независимость же электровозбудительных сил элемента Грове от электролита, растворенного в воде, объясняется тем, что ионы, противодействующие электролитическому растворению водорода и кислорода, это ионы воды Н₂О = Н^· + НО′ и НО′ = Н^· + О″ количество этих ионов в воде определяется электропроводностью самой чистой воды, найденной Кольраушем, равной 0,4·10⁻⁷ обратных омов. Так как электропроводность грамм-эквивалента ионов воды равна сумме их подвижностей, т. е. около 500 (318 + 174), очевидно, один грамм-эквивалент ионов воды, т. е. 1 г иона водорода Н^· и 17 г иона гидроксила НО′ находятся в 500 : 0,4·10⁻⁷ = 1,25·10¹⁰ куб. см, или 1 грамм-эквивалент ионов воды распределен в двенадцати с половиной миллионах литров воды. При прибавлении кислоты или щелочи количество ионов водорода и гидроксила значительно меняется. Кислоты вводят относительно большое число ионов водорода, благодаря этому потенциал водородного электрода понижается по сравнению с таковым в чистой воде, но за то кислоты пропорционально уменьшают количество гидроксильного иона, а следовательно, и иона O″, благодаря этому на величину уменьшения потенциала водородного электрода возрастает электродный потенциал кислорода, сумма же остается та же, т. е. 1,12 вольт. Обратное влияние оказывает на отдельные электроды прибавка щелочи при сохранении того же постоянства общей суммы. Переходя к изучению электродов второго рода, а также необратимых электродов, дóлжно сказать, что движение ионов может вызвать не только химическая реакция растворения электрода металла, но и химическая реакция, происходящая у границы металлического электрода, покрытого нерастворимым, но проводящим веществом, если только вторая часть этой реакции будет происходить у другого электрода. Такими электродами являются пластины металлов, покрытые перекисью свинца, марганца или никеля; они оказывают окислительное действие на вещества, причем продукты окисления должны выделяться у второго электрода. Такие окислительные электроды обладают многими свойствами кислородного электрода, причем кислород уже является как бы сжатым до очень большого давления и поэтому сильно действующим. Кислоты должны подобно их влиянию на кислород-платиновый электрод повышать действие таких электродов. С этим находится в связи известный факт, что электровозбудительная сила обыкновенного свинцового аккумулятора с концентрацией серной кислоты возрастает. Химическая реакция аккумулятора PbO₂ + 2H₂SO₄ + Pb = 2PbSO₄ + 2Н₂О удовлетворяет поставленному выше требованию раздвоенности химической реакция, ибо перекись свинца для реакции берется у одного электрода, а свинец у другого. Наконец, источником электрической энергии может служить свойство ионов менять свою валентность или свой состав; так ион солей закиси железа Fe^·· может перейти в ион соли окиси железа, а ион марганцовой кислоты MnO′₄ может, отдав свой отрицательный заряд, разложиться на перекись марганца и кислород. Электродами для таких электролитов служат опять-таки уголь или платина, причем ни тот, ни другая сами химическому действию не подвергаются. Комбинации таких электродов, к которым налит раствор электролитов, ионы которых в химических реакциях могут менять свою валентность, носят название окислительных или восстановительных цепей. Простейший пример такой цепи будет платиновый электрод, к которому налит раствор соли закиси железа, соединенный с кислород-платиновым электродом. Pt | FeSO₄ | HgSO₄| O₂. В элементе совершается химическая реакция 2FeSO₄ + HgSO₄ + О = Fe₂(SO₄)₃ + H₂С. Кислород, растворяясь, будет образовывать воду, положительные же заряды иона водорода перейдут на платину, ион же SO₄′′ переместится в сторону железного купороса. От платины положительный заряд, пройдя по проводнику, попадет в электролит, изменит ион Fe″ в Fe‴, добавочный положительный заряд которого нейтрализуется перемещением иона SO₄″. Таким образом, ток пойдет во внешнем проводнике от кислород-платины к платине с хлористым железом. Для характеристики свойств окислительных и восстановительных цепей может служить следующее соображение: можно принять, что все восстановители, способные выделять водород из воды, т. е. потенциал которых выше водорода, заряжают платиновый электрод до известной степени газообразным водородом, все окислители обратно заряжают платиновый электрод газообразным кислородом. Следовательно, их отношение к кислотам и щелочам должно быть таково же, как водородного или кислородного электрода, т. е. щелочи должны усиливать восстановительные свойства, а кислоты окислительные. Последнее соображение подтверждается ниже приведенной таблицей отдельных потенциалов, где опять по Нернсту вторым электродом служит водород-платиновая пластинка, погруженная в нормальный раствор соляной кисл.

Электродные или отдельные потенциалы.

Закись олова SnO (щелочное)	0,55
Сернистый натрий Na2S (щелочной)	0,34
Желтая соль K4Fe(CN)6 (щелочной)	−0,23
Двухлористое олово SnCl2 (кислая)	−0,25
Желтая соль K4Fe(CN)6	−0,35
Красная соль К3Fe(CN)6 (щелочн.)	−0,64
Красная соль K3Fe(CN)6	−0,73
Красная соль К3Fe(CN)6 (кислая)	−0,77
Двухромовокислый калий K2Cr2O7	−0,81
Кислород О	−1,12
Хромовая кислота CrO3 (кисл.)	−1,19
Азотная кислота HNO3	от 1,01 до −1,27
Перекись марганца MnO2	−1,38
Марганцево-калиевая соль KMnO4	−1,51
Перекись свинца PbO2 (кисл.)	−1,90

Пользуясь этими данными (в скобках написаны реакции растворов), можно в связи с предыдущими величинами отдельных потенциалов вычислить электровозбудительную силу любого элемента. Как пример можно взять видоизмененный элемента Бунзена: цинк, серная кислота и хромовая смесь, уголь Zn | H₂SO₄ | Н₂Cr₂О₇ | С. Согласно таблице получается 0,77 − (−1,19) = 1,96. На практике такие элементы дают до 2,00 вольт. Величина электровозбудительноа силы окислительных цепей зависит от концентрации иона, производящего окисление. Зависимость эта логарифмическая, т. е. электровозбудительная сила возрастает очень медленно с увеличением концентрации иона. Этим отчасти объясняется падение электровозбудительных сил окислительных элементов по мере их работы, этим же в связи с повышением кислотности объясняется также возрастание абсолютного числа электровозбудительной силы азотной кислоты от 1,01 до 1,27.

Энергетические соотношения. В период, когда создавалось учение об энергии, независимо Гельмгольц (1847) и Вильям Томсон (1851) высказали закон, потребовавший впоследствии некоторых изменений, гласящий, что возможный максимум электрической энергии гальванического элемента эквивалентен количеству теплоты, которое выделяется при химических реакциях, совершающихся в данном гальваническом элементе. Следовательно, согласно первоначальной формулировке закона, вся теплота, получаемая при химических процессах, может быть переведена в электрическую энергию. Расчет, произведенный для гальванического элемента Даниеля, как бы подтвердил это предположение. Электролитические расчеты удобнее всего вести с грамм-эквивалентами веществ. Количество электричества, которое выделяется при химическом превращении с грамм-эквивалентом вещества, равно F, т. е. 96580 кулонов, а электр. энергия, очевидно, Е — 96580 джоулей или 0,239·Е·96580, т. е. 23100·Е калорий, где Е электровозбудительная сила в вольтах. Химическая реакция элемента Даниеля Zn | ZnSO₄| CuSO₄ | Cu, состоит в вытеснении меди цинком. Цинк растворяется, медь оседает по уравнению Zn + CuSO₄ = Cu + ZnSO₄. При растворении грамм-эквивалента цинка, т. е. 32,7 граммов, и выделении грамм-эквивалента меди, т. е. 31,8 граммов, развивается 25055 калорий тепла. Теплота этой реакции определена Яном в условиях действия элемента Даниеля. Он нашел ее, замыкая ток и помещая весь элемент вместе с замкнутой цепью в калориметр. Если только вся теплота переходит в электрическую энергию, тогда 25055 = Е·23100, где Е электродвижущая сила элемента Даниеля, исследованного Яном. Откуда она получается равной 1,085 вольт. Измеряя ее для того же элемента, Ян получил 1,094, т. е. величину весьма близкую к теоретической. Гельмгольц и Томсон не располагали превосходными измерениями, произведенными Яном, и их расчеты привели к полному тождеству наблюденной и вычисленной электровозбудительной силы. Однако вскоре в 1882 г. Гельмгольц, подметив, что электродвижущая сила многих элементов значительно меняется с температурой, теплота же химического превращения остается при этом постоянной, видоизменил первоначальный закон. Закон в его первоначальной форме и до сих пор находит себе применение для приблизительных расчетов электровозбудительных сил и известен под названием закона Томсона. Согласно новым, теперь общепринятым воззрениям Гельмгольца, теплота, выделяющаяся при химических превращениях, —результат двух разнородных частей одной и той же химической энергии. Одна часть химической энергии переходит в электрическую и носит название обратимой части (А), другая переходит только в тепловую энергию —необратимая часть (B). Возможны случаи, когда B является отрицательной величиной, т. е. благодаря действию обратимой части химической энергии данная система охлаждается или поглощает теплоту из окружающей среды. Таким элементом, например, является вышеупомянутый элемент Даниеля. Его электрическая работоспособность (А) равна 1,0936 х 23100, т. е. 25263 кал.; а теплота реакции только 25055 кал. Заслуга Гельмгольца заключается в том, что, пользуясь вторым принципом термодинамики, он показал, как вычислить величину В из изменения электровозбудительной силы элемента с изменением температуры, т. е. из температурного коэффициента $\left({\frac {dE}{dT}}\right)$, где dE обозначает изменение электровозбудительной силы, a dT изменение температуры. Гельмгольц теоретически вывел, что $B=-23100,T{\frac {dE}{dT}}''$. Ян нашел для своего элемента температурный коэффициент, равный 34·10⁻⁶; отсюда В = — 23100·T·34·10⁻⁶, т. е. −214 калорий. Таким образом, вычисляется общий тепловой эффект элемента Даниеля (q) равным А + В, т. е. q = 25263−214 или 25049 калорий, найденный же опытом равен 25055, что составляет совпадение, далеко превосходящее возможные ошибки опыта. Закон Гельмгольца привел к весьма знаменательному в истории науки событию. Современные термохимические (см. Термохимия) расчеты основаны отчасти на систематических исследованиях Томсона. Оказалось, что данные Томсона для ртутных солей не совпали с данными, вычисляемыми по закону Гельмгольца из величин электровозбудительных сил гальванических элементов с ртутными электродами и ртутными солями. Оствальд предположил возможность ошибки в данных Томсона. Была сделана проверка данных самим Томсоном и независимо Нернстом, подтвердившая предположение Оствальда. Полученные новые величины совпали с предвычисленными по теории Гельмгольца. Теорией Гельмгольца можно воспользоваться для расчета отдельных электродных потенциалов на границе металл и раствор соли того же металла, пользуясь термохимическими данными. Такие расчеты бели произведены Вильсмором и другими исследователями для солей щелочных и щелочноземельных металлов, приравнивая теплоту их превращения обратимой части химической энергии. Непосредственное измерение необратимой части энергии (величины В) электрическим путем невозможно, ибо для разлагающих воду металлов не удается определять самой величины электродвижущей силы. Подметив, что для большинства хлористых солей В постоянно и близко 6000 калориям, для бромистых близко к 4850 калориям, для йодистых близко 690 калориям, я предположил, что необратимая часть энергии В для солей щелочных металлов остается той же величиной. Вычисления отдельных потенциалов из теплот образования хлористых солей были сделаны по формуле $Q=(\varepsilon _{h}+1,42)\cdot 23100+6000$, где Q теплота реакции образования раствора соли из хлора и металла в малых калориях; $\varepsilon _{h}$ искомый отдельный потенциал, отнесенный к водородному электроду; 1,42 — отдельный потенциал хлора. Подобными же формулами были вычислены величины $\varepsilon _{h}$ из бромистых и йодистых солей. Данные для отдельных потенциалов совпали и получились для:

Калия К	2,69
Натрия Na	2,49
Бария Ва	2,58
Стронция Sr	2,55
Кальция Са	2,38
Магния Mg	2,37

Эти величины показывают, насколько электровозбудительная сила элементов с металлическим калием или натрием, если бы таковой удалось устроить, была бы больше, хотя бы, цинковых элементов. Величины для В делают также вероятным, что электровозбудительная сила таких элементов с повышением температуры уменьшается.

Классификация гальванических элементов. 1. а) Гельмгольцевский концентрационный элемент. Металлические электроды погружены в соприкасающиеся растворы разной концентрации солей того же металла. Пример такого элемента представляет серебро | концентрированный раствор азотнокислого серебра | разбавленный раствор той же соли | снова серебро +Ag | AgNO₃ ➸(концентриров.) | AgNO₃ (разбавленный) | Ag. Противодействие осмотического давления ионов электролитическому растворению серебра, очевидно, меньше в разбавленных растворах, поэтому серебро будет растворяться в разбавленном растворе и оседать в концентрированном. Благодаря этому серебро в разбавленном растворе будет отдавать вместе с ионом Ag^· раствору положительное электричество и само электризоваться отрицательно. Знаки + и − в схеме показывают полюсы элемента, а стрелка — направление тока во внешней цепи. Если пренебречь концентрационным током на границе электролитов, тогда формула для элемента получается очень просто. $E=\varepsilon _{2}-\varepsilon _{1}$>, где $\varepsilon _{2}$ электровозбудительная сила на границе разбавленного раствора электролита и металла, а $\varepsilon _{1}$ — электродвижущая сила на границе концентрированного раствора и металла. Согласно выше упомянутой теории Нернста, для темп. 18°, для одноэквивалентных металлов $\varepsilon =0,577\lg {\frac {P}{p}}$. Если для $\varepsilon _{2}$ осмотическое давление ионов равно $p_{2}$, а для границы с $\varepsilon _{1}$ равно $p_{1}$ тогда $E=0,0577\lg {\frac {P}{p_{2}}}-0,0577\lg {\frac {P}{p_{1}}}=0,0577\lg {\frac {p_{1}}{p_{2}}}$. Если брать оба раствора такой концентрации, чтобы можно было считать степень электролитической диссоциации солей одинаковой, тогда $p_{2}$ и $p_{1}$ можно считать пропорциональным концентрации соли $c_{2}$ и $c_{1}$ и получается формула $E=0,0557\lg {\frac {c_{1}}{c_{2}}}$. Если скорости переноса аниона и катиона мало отличаются, как в одном ниже приведенном случае, тогда можно для расчета применять эту формулу, если же они отличны, тогда нужно ввести поправку на электродвижущую силу на границе электролитов концентрации $c_{1}$ и $c_{2}$, и формула принимает, согласно Нернсту, вид $E=0,0577{\frac {2v}{u+v}}\log {\frac {c_{1}}{c_{2}}}$, где v и u подвижности ионов (см. главу Перенос ионов); для нашего случая u серебра, a v иона NO₃′; 2v = 121,6, a v + u = 116,5 (см. соотв. таблицу цитиров. главы). Для отношения ${\frac {c_{1}}{c_{2}}}=10$, т. е. когда один раствор в десять раз крепче другого, Е вычисляется равным 0,06 вольта. Опыт дает 0,055 вольт. Если ввести поправку на степень электролитической диссоциации, пользуясь формулой Аррениуса, тогда получается еще лучшее совпадение, именно, вычисляется E = 0,057 вольт. При большой разнице концентраций электровозбудительная сила таких элементов достигает значительных величин. Примером тому может служить уже давно известный элемент серебро | раствор соли азотнокислого серебра | раствор хлористого калия | серебро — Ag | AgNO₃ | KCl | Ag. Присутствие хлористого калия у серебряного электрода понижает и без того малую растворимость хлористого серебра, это понижение достигается действием иона хлора (см. Электролитическая диссоциация). Если концентрация хлористого калия будет грамм-эквивалент в литре, тогда, по закону действия химических масс, концентрация хлористого серебра изменится в квадрате, т. е. из 1,1·10^—5 нормальной (0,00015%, см. Электрохимический анализ) сделается 1,21·10⁻¹⁰ нормальной. Для такого элемента можно применить упрощенную формулу, пренебрегая электровозбудительной силой на границе азотнокислого серебра и хлористого калия. Для случая, когда будет взята концентрация азотнокислого серебра 0,1 нормальной, т. е. 17 грамм в литре, формула примет вид $E=0,0577\log {\frac {0,1}{1,21\cdot 10^{-10}}}$. Этой формулой вычисляется электровозбудительная сила, равная 0,52 вольт, а опыт дает 0,51. b) Нернст исследовал целый ряд более сложных концентрационных цепей и разработал их теорию. Такие элементы получаются при применении электродов второго рода или целого ряда электролитов с разными ионами. Теоретические расчеты Нернста совпали с опытными данными. с) К совершенно своеобразным концентрационным элементам должно отнести элементы, предложенные Г. Мейером и Тюриным. В этих элементах меняется не концентрация электролита, а концентрация вещества самого электрода, так что в формуле Нернста $E=n^{-1}0,0577\log {\frac {P}{p}}$ меняется не p — сила противодействия ионов растворению, а Р, т. е. сама электролитическая упругость растворения металла. В этом отношении описываемые элементы напоминают газовые (см. ниже). Изменение P достигается применением в качестве электродов двух амальгам одного и того же металла, но разной концентрации, причем электролитом в элементах Г. Мейера служат соли растворенного металла, а в элементе Тюрина ртутные соли. В элементе Г. Мейера действующим началом является растворенный в ртути металл, упругость электролитического растворения его должна быть больше ртути. В элементе Тюрина действует сама ртуть, так как в ней растворяют металлы, упругость электролитического растворения которых меньше ртути. Теория этих элементов дана их авторами и для элементов Г. Мейера проверена на опыте.

2. Самый распространенный тип элементов составляют элементы с обратимыми электродами первого и второго рода (см. Электроды). а) К этим элементам относятся элементы типа Даниеля: металл | соль металла | соль второго металла | второй металл. К этим же элементам относятся описанные выше нормальные элементы, напр., элементы Гельмгольца: Zn | ZnCl₂ | HgCl | Hg, где HgCl | Hg является обратимым электродом 2-го рода. Электровозбудит. сила элем. типа Даниеля для 18° вычисляется по формуле Нернста $E=n^{-1}0,0577\log {\frac {P_{1}}{p_{1}}}-n^{-1}0,0577\log {\frac {P_{2}}{p_{2}}}$, где n для меди и цинка равен двум. Эта формула верна, если пренебречь малой электродвижущей силой на границе электролитов. При нормальных концентрациях, для которых осмотические давления ионов (р) одинаковы и при $P_{1}>P_{2},$ $E_{H}=n^{-1}0,0577\log {\frac {P_{1}}{p}}-n^{-1}0,0577\log {\frac {P_{2}}{p}}$; отсюда $E_{H}-E=n^{-1}0,0577\log {\frac {p_{2}}{p_{1}}}$, т. е. увеличение концентрации соли у электрода с меньшей упругостью электролитич. растворения увеличивает электровозбудит. силу на $n^{-1}0,0577\log {\frac {p_{2}}{p}}$, и на ту же величину уменьшает электродвижущую силу, увеличение концентрации соли металла электрода большей электролитической растворимости вблизи электрода. Приблизительный расчет величины электродвижущей силы этих элементов, пренебрегая концентрационными токами, можно сделать формулой $E_{H}=\varepsilon _{h}-\varepsilon _{h2}$, т. е. вместо абсолютных потенциалов приведенных формул можно пользоваться «Нернстовскими» отдельными потенциалами. Так, для элемента Даниеля получится E₁ = 0,77 − (−0,33) = 1,1 вольт, для элемента Гельмгольца E₂ = 0,77 − (−0,283) = 1,053 вольт, −0,283 потенциал ртутного каломельного электрода. Последняя величина E₂ требует еще значительной поправки, зависящей от концентраций электролитов, ибо опыт дает для элемента Гельмгольца только один вольт. Чтобы ввести эти поправки опять таки пользуются для каждого электрода формулой Нернста $n^{-1}0,0577\log {\frac {p_{2}}{p}}$ или проще $n^{-1}0,0577\log x$, где отношение осмотического давления к нормальному давлению заменяют отношением концентраций (х) данной и нормальной (грамм-эквивалент в литре). b) К тому же типу элементов должно отнести так называемые анормальные гальванические элементы. Они отличаются от элементов а-2-го типа только необыкновенно низкой концентрацией ионов у электрода с меньшей упругостью растворения, так что благодаря этому даже меняется направление тока. Пример такого элемента цинк | цинковый купорос водный | водный цианистый калий | медь, Zn | ZnSO₄ | KCN | Cu. В этом элементе ток идет не от меди к цинку, как в элементе Даниеля, а, наоборот, от цинка к меди, не цинк растворяется, а медь осаждается, напротив медь вытесняет цинк. Такой элемент является блестящей иллюстрацией теории Нернста. Цианистый калий настолько понижает концентрацию ионов меди, что в формуле Нернста $E=n^{-1}0,0577\left(\log {\frac {P_{1}}{p_{1}}}-\log {\frac {P_{2}}{p_{2}}}\right)$ величина ${\frac {P_{2}}{p_{2}}}$, благодаря очень малой $p_{2}$, делается больше, чем величина ${\frac {P_{2}}{p_{2}}}$. Нужно заметить, что величина $p_{2}$ должна быть очень мала. Это видно из того, что $E=n^{-1}0,0577\log {\frac {P_{1}}{P_{2}}}$, если $p_{1}=p_{2}=1$, т. е. взяты нормальные концентрации. Отношение $P_{1}:P_{2}$ вычисляется из равенства $1,1={\tfrac {1}{2}}0,0577\log {\frac {P_{1}}{P_{2}}}$, где 1,1 электровозбудительная сила элемента Даниеля, равным 10³⁸. Та же величина получится делением упругостей растворения цинка и меди, приведенных в ст. Электролитическая растворимость.

с) Газовые элементы. Они устраиваются с платиновыми электродами, погруженными частью в газ, частью в раствор электролита, напр., элемент Грове, и представляют тоже элементы с обратимыми электродами 1-го рода. Упругость газа, а следовательно, и степень насыщенности газами платины, служащей посредницей между жидкой и газообразной средой, определяет электродвижущую силу таких элементов. Другими словами, каждый газовый элемент является концентрационным элементом типа Г. Мейера. Можно считать с большой вероятностью, что величина упругости газа, если он насытил при данной своей упругости поверхность платинового электрода, пропорциональна величине Р формулы Нернста, т. е. электролитическая упругость растворения (Р) пропорционально возрастает с упругостью газа.

3. Элементы с окислителями у электродов. а) Сюда относится большинство элементов, применяющихся в ежедневной практике, например элемент Грове: цинк | серная кислота | азотная кислота | платина; элемент Бунзена: цинк | серная кислота | азотная кисл. | уголь; хромовый элемент: цинк | серная кислота | хромовая кислота с серной кисл. | уголь (см. Гальванические элементы). К вышеизложенным теориям должно прибавить, что эти элементы не отличаются постоянством, главным образом потому, что по мере нейтрализации кислоты и химического разложения окислителя потенциал у электрода окислителя значительно меняется. Достаточно привести, хотя бы, свойства элемента Грове; электродный потенциал его азотной кислоты меняется в пределах от 1,01 до 1,27. Следовательно, теоретически колебания его электродвижущей силы равны приблизительно 0,77 (для цинка) + 1,01 или + 1,27, т. е. от 1,78 до 2,04 вольт. На практике наблюдают величины электродвижущей силы от 1,8 до 1,9 вольт, что объясняется тем, что элементы не наполняют концентрированной 95% азотной кислотой, для которой найдена величина 1,27, но берут обыкновенно 53 % азотную кислоту (уд. веса 1,33). b) К этим элементам должно отнести и угольный элемент. Термохимические данные сгорания грамм-эквивалента (3 грамма) углерода позволяют предвычислить электродвижущую силу угольного элемента. При сжигании трех грамм обыкновенного угля получено 24200 калорий (для графита и алмаза получены немного меньшие величины). Отсюда электродвижущая сила реакции: С + О₂ = СО₂, если только всю химическую энергию перевести в электрическую, вычисляется E·23100 = 24200 или Е близко одному вольту. Однако уголь при обыкновенной температуре не удается перевести в ион, в известных растворителях он играет вполне индифферентную роль, как бы не обладает никакой упругостью электролитического растворения. По-видимому, поэтому вопрос об использовании энергии химического соединения угля с каким-либо элементом при обыкновенной температуре вряд ли можно считать имеющим будущее. Совершенно иное нужно сказать о попытках, произведенных при высоких температурах. Основной принцип, которому должно следовать при устройстве угольных элементов: окислитель угля должен находиться непременно у другого электрода гальванического элемента, чтобы таким образом разбить химическую реакцию на две части (см. главу Переход химич. энергии в электрическую). Угольный элемент Яблочкова и многие другие не удовлетворяли этим требованиям. Наблюдавшаяся в таких элементах электродвижущая сила по всей вероятности была термоэлектрического характера. Требованию современных теорий уже удовлетворяют элементы Coehn и Jacques. Схема последнего элемента: железо | (кислород) окись железа | едкое кали | уголь ретортный. Железо покрыто слоем окиси, возобновляемой током кислорода. При нагревании, по-видимому, выше красного каления окись железа отдает часть кислорода едкому кали (по всей вероятности, в виде иона O″), а едкое кали этим кислородом при той же высокой температуре окисляет уголь. Однако легко убедиться в непригодности такого элемента. В реакциях этого элемента участвует вода и углекислота. По мере действия этого элемента количество воды, благодаря испарению, уменьшается, а количество углекислоты увеличивается и едкое кали по реакции 2КНО + CO₂ = K₂CO₃ + H₂O превратится в поташ. Такие свойства этого элемента сделали его не применимым в технике, несмотря на блестящие результаты первых опытов. Дóлжно, таким образом, считать, что не существует приложимых на практике угольных элементов. Элементы Борхерса и многие другие, в которых продукты неполного сгорания угля, т. е. окись углерода (СО) при дальнейшем сгорании по реакции СО + О = CO₂ должны были давать гальванический ток, оказались также мертворожденными. В этой области, при значительном накопившемся материале, как бы недостает таланта или гения, чтобы отыскать правильный путь и сделать по этому пути верный шаг вперед.

Электролиз и поляризация. Химическое разложение током электролитов было названо Фарадеем электролиз. При движении ионов в электролитах они сохраняют свои электрические заряды, а потому никаких химических изменений, связанных с уменьшением числа этих зарядов, не наблюдается. Такие изменения наступают только у электродов, где ионы, отдавая электродам свои электрические заряды, могут или целиком выделиться, как таковые, напр., ионы металлов, йод, бром и др., или изменить число зарядов, находящихся на ионе; так напр., при электролизе концентрированного раствора желтой соли K₄FeCy₆ ион её FeCy₆″″ у анода переходит в FeCy₆′′′, отдавая аноду один заряд, т. е. окисляясь в ион красной соли (K₃FeCy₆); или, наконец, ион, отдав свой заряд, может разложиться, как при электролизе марганцевокислого калия MnO₄′ с выделением перекиси марганца. При электролизе органических кислот ионы их разлагаются, так напр., ион уксусной кислоты, согласно исследованиям Кольбе и Бунге, на углекислоту (СО₂) и этан (С₂Н₆) по уравнению:

2C₂H₃O₂′ = C₂H₆ + 2CO₂,

при этом, конечно, электрический заряд, обозначенный черточкой иона, переходит на электрод. Для выделения иона на электроде, собственно для отделения иона от его заряда, должно теоретически затратить ту же электрическую энергию, которая развивается при переходе данного иона в раствор. Энергия измеряется произведением количества электричества на электровозбудительную силу, а так как количество электричества пропорционально, по закону Фарадея, количеству разложившегося вещества, то, очевидно, не количеством электричества определяется возможность наступления электролиза при данном запасе электрической энергии, а только применяемой электродвижущей силой. Очевидно, что нельзя разложить вещество электродвижущей силой меньше той, которую развивают в условиях опыта продукты разложения. Поэтому вышеприведенные величины для электродных потенциалов являются также характерными величинами для минимума электровозбудительных сил, необходимых для разложения соответствующих солей. Как пример можно привести хлористый кадмий (CdCl₂). Для наступления разложения его между платиновыми электродами Ле Блан нашел непосредственным опытом электровозбудительную силу в 1,88 вольт. Электровозбудительная же сила элемента: кадмий | хлористый кадмий | хлор вычисляется согласно вышеприведенным электродным потенциалам равной 1,82 вольт. Понятно, что опыт определения электродвижущей силы, необходимой для разложения, всегда даст немного большие величины, чем вычисляемые из электродных потенциалов, так как в момент, когда электродвижущая сила равна 1,82, электролиз фактически еще не наступает. Долгое время как бы противоречием этим основным положениям считали факт прохождения через раствор токов электровозбудительных сил меньших тех, которые необходимы для разложения данного электролита. Прохождение такого тока длится, правда, короткое время. Клаузиус, чтобы объяснить это явление, считал необходимым признать, что ничтожная часть электролита в растворе уже находится в химически разложенном состоянии. Понятие о возможности движения свободных ионов внутри электролита, помимо каких бы то ни было химических превращений, было введено в науку Гельмгольцем; впоследствии оно стало основным положением теории электролитической диссоциации Аррениуса. Согласно Гельмгольцу, при прохождении токов малых электродвижущих сил ионы доходят до электродов, накопляются там в виде двойного электролитического слоя, причем предел их накопления обусловливается величиной действующей электродвижущей силы; до достижении этого предела ток прекращается. Такое прекращение тока, согласно установившейся раньше терминологии, объяснялось поляризацией электродов. Ясно, что здесь наступает своеобразная поляризация, которую должно назвать ионной поляризацией. Величину её можно определить, выключая из цепи действующую электровозбудительную силу и замыкая цепь на приборы для измерения электродвижущих сил. В пределе величина такой поляризации равна первоначально действовавшей электровозбудительной силе. Если теперь постепенно увеличивать электродвижущую силу, тогда наступит момент при известной её величине, когда ток поляризацией не прекратится и по проводникам пройдет длящийся ток. Этот момент и соответствует наступлению электролиза, а наблюденная электровозбудительная сила носит название электровозбудительной силы разложения и, как уже выше сказано, минимум её совпадет с величинами электродных потенциалов. При электролизе более или менее концентрированных растворов электролитов нужно принять во внимание вышеупомянутые изменения электродных потенциалов в зависимости от концентраций, согласно формуле Нернста, $\varepsilon =n^{-1}0,057\log {\frac {P}{p}}$. При уменьшении p, т. е. осмотического давления и, следовательно, концентрации, величина ε возрастает, т. е. нужно применять большую электродвижущую силу при электролизе разбавленных растворов. Этим не исчерпываются явления электролиза. При дальнейшем усилении тока величина электродвижущей силы, противодействующей току, не остается постоянной, но возрастает, Явление возрастания этой противодействующей силы опять-таки носит название поляризации. Эта поляризация собственно и представляет настоящую концентрационную поляризацию. Причина её — постоянное выделение ионов электролизуемого вещества у электрода и, следовательно, уменьшение их концентраций, весьма заметное у самого электрода. Такое уменьшение концентрации увеличивает, по Нернсту, величину электродных потенциалов. Нернст и Глазер, подробно изучая ход электролиза, наблюдали, что, по мере усиления тока с увеличением электродвижущей силы, может наступить новый момент в изменении характера электролиза: иона, первоначально выделявшегося, как бы не будет хватать для электролиза и начнет выделяться ион с большим электродным потенциалом. При электролизе водного раствора йодистоводородной кислоты сначала будет выделяться йод, если же ток значительно усилить, тогда начнет выделяться также и кислород. Для разложения йодистоводородной кислоты нужна минимальная электродвижущая сила, равная 0,52 вольт, а для наступления разложения воды в условиях опыта, по крайней мере, 1,12 вольт. Такое толкование электролиза выясняет качественную сторону отдельных случаев химического разложения током различных электролитов. Основное положение формулируется: ток выделяет из раствора ион с меньшим электродным потенциалом. При электролизе растворов едкого кали, у катода выделяется не металлический калий, а водород. Причина та, что электродный потенциал калия 2,69 лежит значительно выше нуля, принимаемого для водорода. При электролизе серной кислоты слабыми токами выделяется кислород непосредственно изменением кислородного иона (воды) в газообразный кислород с потерей двух отрицательных зарядов. Найдено, что уже электродвижущая сила в 1,12 вольт разлагает водные растворы серной кислоты. При дальнейшем усилении тока наступает момент, когда совершается то превращение, которым обычно разъясняют электролиз серной кислоты. Концентрация ионов кислорода и без того очень малая (см. выше главу Переход химической в электрическ.) при усилении тока настолько уменьшается у электрода, а электровозбудительная сила, необходимая для выделения ионов, настолько возрастает, что, наконец, начинает непосредственно выделяться ион серной кислоты SO₄″. Этот ион с потерей заряда распадается по уравнению SO₄ + Н₂О = Н₂SO₄ + O с выделением кислорода. В первом случае непосредственного выделения иона кислорода получается как бы прямое разложение током воды, однако, при этом необходимо помнить, что током переносятся почти исключительно ионы серной кислоты, и механизм самого электролиза объясняется переносом исключительно ионов серной кислоты (число ионов кислорода в биллионы раз меньше числа ионов серной кислоты) и только у электродов, благодаря громадному электродному потенциалу ионов SO₄″, близкому к 1,9 вольт, сначала выделяются ионы кислорода, а впоследствии, когда соотношение концентраций кислорода и иона остатка серной кислоты достигает величин приблизительно 10²⁷, наступает непосредственное выделение иона серной кислоты. Последнюю величину 10²⁷ можно приблизительно вычислить по вышеприведенной формуле $\varepsilon _{2}-\varepsilon _{1}=n^{-1}0,0577\log {\frac {p_{2}}{p_{1}}}$, где $\varepsilon _{2}=1,9$; $\varepsilon _{1}=1,12$, $n=2$, ибо O и SO₄ двуэквивалентны, в предположении, что отношение осмотических давлений ${\frac {p_{2}}{p_{1}}}$ при очень малых концентрациях соответствует отношению концентраций. Когда продуктами электролиза являются газообразные вещества, явления усложняются тем обстоятельством, что упругость выделяемых газов влияет на величину электродных потенциалов, а следовательно, и на величину электровозбудительной силы, необходимой для превращения данного иона в газообразное вещество. Этим объясняется своеобразное открытие, сделанное А. П. Соколовым, что при известных условиях воду можно разложить малой электродвижущей силой, меньшей 1,12 вольт. Для того, чтобы получить такое разложение, нужно понизить упругость газов над водой значительно ниже атмосферного давления, другими словами, производить электролиз в безвоздушном пространстве. Понятно, что этим не нарушается принцип, высказанный выше, так как, в свою очередь, соединяясь при малой упругости, кислород и водород дадут тоже меньшую электродвижущую силу. При электролизе с газообразными продуктами большую роль играет также способность данного металла поглощать газы. Очевидно, если только поверхности металлов обладают ничтожно малой способностью поглощать газы и легко образуют как бы пересыщенные растворы газов, величины электродвижущих сил, которые придется затратить на такой поверхности для перехода иона в газообразное состояние, могут значительно возрасти. Этим могут быть объяснены анормальные потенциалы для выделения газов, хотя бы, на ртутной поверхности. Для заметного выделения водорода при атмосферном давлении на ртути нужна электродвижущая сила на 0,76 вольт больше теоретической, т. е. наблюденной на платинированном платиновом электроде. Известный факт амальгамирования цинка ртутью для предохранения его от действия кислот объясняется только ненормальным потенциалом выделения водорода на ртутной поверхности; иначе ртуть должна была бы подобно свинцу (см. Электролитическая растворимость) ускорять растворение цинка. Значительно проще явления у так называемых не поляризующихся или обратимых металлических электродов 1-го рода (см. Электроды). При электролизе соли металла между металлическими же поверхностями току никаких электродвижущих сил, кроме вызываемых разницей концентрации, соответствующих, следовательно, по своим величинам Гельмгольцевскому концентрационному элементу, преодолевать не приходится. Электровозбудительная сила выделения металла у катода при равенстве концентрации соли данного металла равна и противоположна электровозбудит. силе его растворения у анода.

Современные электрохимические теории. Электрохимич. теории прошлого, изложенные в главе Историческая справка, в свое время принесли огромную пользу химии, однако они были окончательно оставлены во второй половине прошлого века. Блестящие открытия в области органической химии, где электролиты играют второстепенную роль, отодвинули на второй план электрохимию, и все внимание ученых и техников сосредоточилось на органической химии. Возрождение электрохимии обязано, главным образом, исследованиям физического характера. Гельмгольц в 1881 г., в своей речи, посвященной памяти Фарадея, положил первые краеугольные камни современной электрохимии: Дэви и Берцелиус в своих теориях спекулировали с количеством электричества на атоме, величиной, которая, как показали позднейшие исследования, одинакова для единичного заряда всех атомов; причем только заряды атомов могут быть двойные и тройные, соответствующие их валентности. Один факт одинаковости величины зарядов атомов делал все спекуляции Дэви и Берцелиуса непригодными для современной электрохимии. Гельмгольц подчеркнул это постоянство величины заряда, предположив, что, быть может, и электричество обладает атомистическим строением, причем величина атома электричества равна 9658010²⁴ или прибл. 1·10⁻¹⁹, где 10²⁴ обозначает предполагаемое абсолютное число атомов в грамм-молекуле одноэквивалентного вещества. Величину такого заряда называют теперь электроном, обозначая для положительного электричества ⊕ и для отрицательного ⊖. Между электроном и атомами происходит реакции, подобно происходящим между атомами. Так, ион водорода на электроде теряет электрон до уравнению H· = H + ⊕, превращаясь в газообразный водород; при этом непременно должен образоваться и отрицательный электрон, т. е. на другом электроде ион хлора превращается в газообразный хлор Cl′ = Cl + ⊖. Эти превращения совершаются при электролизе. При образовании соляной кислоты из хлора и водорода, атомы, благодаря сродству к электричеству, соединяются с электронами, разлагая нейтральные электроны ⊖, которыми заводнено мировое пространство, Таким образом, количества электричества не могут лечь в основание современных спекуляций о свойствах атомов, ибо одиночные заряды его везде одинаковы, Современные спекуляции базируют на другом факторе электрической энергии, именно, на электродвижущей силе. Оствальд впервые ясно формулировал основное положение, что направление химической реакции определяется величиной её электродвижущей силы. Изменение данной системы химических веществ идет не в сторону большого выделения тепла, как полагал Бертело (см. Термохимия), а в сторону наибольшей электрической работы и, следоват., наибольшей электродвижущей силы. Другими словами, при небольщих разницах концентраций ионов двух металлов, каждый металл с большим электродным потенциалом выделяет из солей металл с меньшим электродным потенциалом. При изучении зависимости направления реакции от величины электродных потенциалов должно, во-первых, помнить, что их можно применять только к теоретически возможным реакциям и, во-вторых, что электродвижущая сила каждой реакции вычисляется, по крайней мере, из двух электродных потенциалов, наблюдаемых у двух электродов. В случае металлов дело упрощается, ибо продукты реакции всегда определенные соли металлов. При изучении окислительных и иных реакций удобнее всего, во избежание недоразумений, определив предполагаемую реакцию, теоретически конструировать соответствующий элемент. Легко, например, из выше приведенных данных для отдельных потенциалов вывести факты, что кислород будет окислять соли закиси железа в соли окиси, но не будет окислять солей окиси хрома в водных растворах в хромовую кислоту и т. п. Доказательством тому, что электродвижущая сила, а не тепловой эффект определяют направление реакции, могут служить весьма характерные факты, когда совершается химическое превращение с поглощением тепла. Таким превращением будет, например, выделение свинца из его азотнокислых солей талием. Элемент: талий | водный раствор азотнокислого талия | водный раствор азотнокислого свинца | свинец будет обладать электродвижущей силой, равной 0,19 вольт, следовательно, в состоянии отдать проводникам при растворении грамм-эквивалента талия энергию, равную 0,19·23100 или 4390 калорий. А так как реакция вытеснения свинца талием идет с незначительным поглощением теплоты, следовательно, элемент будет во время работы охлаждаться. Из этого факта ясно видно, что только обратимая часть энергии, равная для нашего примера 4390 калорий, а не тепловой эффект определяют направление химического превращения. Величина электровозбудительной силы является настолько характерной для данного превращения, что Оствальд предложил прибор, приспособленный для измерения электровозбудительных сил, т. е. электрометр, назвать хемометром. Очевидно, что выше приведенные величины электродных потенциалов металлов и иных простых тел харатеризуют до известной степени их реакционную способность. Электродные потенциалы простых тел представляют настолько характерные величины, что стремятся найти зависимости между такими потенциалами и другими свойствами электролитов. Абегг и Бодлендер показали, что большая степень ионизации присуща солям, образованным из ионов с большими электродными потенциалами. Соли щелочных металлов, в общем, больше ионизированы, чем соли цинка, кадмия и меди, а последние больше, чем соли ртути и серебра. Соли же золота и платины почти не ионизируют с образованием ионов золота и платины. В общих чертах растворимость, солей тоже показывает отдаленное соотношение с электродными потенциалами. Так, почти все соли щелочных металлов растворимы, соли же серебра, как хлористое, бромистое и йодистое, мало растворимы. Исключения из этого правила объясняются отчасти способностью молекул образовывать двойные, тройные молекулы и химически соединяться с молекулами других солей, т. е. образовывать комплексные молекулы. Так, соли цинка и кадмия обладают большей растворимостью, быть может, благодаря тому, что их молекулы способны к образованию более сложных молекул. Соли же платины и золота в водных растворах известны только в виде комплексных солей и химически чистое хлорное золото или четыреххлорная платина при растворении в воде реагирует с ней, образуя, как показал Гитторф, своеобразные кислоты. Кроме непосредственной, выше изложенной характеристики реакционной способности простых тел, электродные потенциалы могут служить для классификации и иных химических свойств электролитов. Абегг и Бодлендер подметили, что чем меньше электродные потенциалы ионов данного электролита, тем резче выражено его стремление к образованию сложных комплексных ионов. Соли щелочных металлов не образуют между собой двойных солей и комплексных ионов. Для щелочноземельных уже небольшое число двойных солей известно; правда, в водных растворах они нацело распадаются на составляющие их соли. Для солей цинка и кадмия уже известны не только двойные соли, но и комплексные ионы этих солей в водных растворах типа CdCl₄″ для хлористого кадмия; все же соли платины и золота, как выше упомянуто, почти нацело ионизируют на комплексные ионы. Например, хлороплатинат натрия Na₂PtCl₆ в самых разбавленных растворах ионизирует только на 2Na^· и PtCl₆″. Такое же влияние оказывают и слабые анионы. Так, соли синильной кислоты всех тяжелых металлов образуют весьма прочные комплексы, чему примером могут служить многократно упоминавшиеся желтая и красная соли железа. В заключение должно сказать, что большинство идей современной электрохимии еще не закристаллизовались в формы, которые принято называть законами природы. Должно помнить, что современная электрохимия еще не праздновала двадцать пятого года своего существования, если даже отнести день её рождения к знаменитой Фарадеевской лекции Гельмгольца. Однако эти идеи причастны общему научно философскому движению. Философская мысль, хотя бы новая философия Оствальда, и ежедневная научная работа уже многое почерпают из этой молодой дисциплины.

Литература. Ostwald, «Elektrochemie, ihre Geschichte und Lehre»; Arrhenius, «Lehrbuch der Elektrochemie» (перевод со шведского); Ahrens, «Handbuch der Elektrochemie»; Minet, «Traité théoretique et pratique d’Electro-Chimie»; Lüpke, «Grundzüge der Elektrochemie» (рус. перевод); Haber, «Grundriss der technischen Elektrochemie»; И. А. Каблуков, «Основные начала физической химии. 2-ой выпуск. Электрохимия». Кроме того, имеются немецкие учебники: Le Blanc, Jahn, Frechland, Löb и Vogel und Rössing. Nernst und Borchers издают «Jahrbuch der Elektrochemie»; Abegg редактирует «Zeitschrift für Elektrochemie». Литература отделов Э.: Kohlrausch und Holborn, «Leitvermögen der Elektrolyte»; И. A. Каблуков, «Очерки из истории электрохимии»; А. П. Соколов, «Современное состояние наших сведений об электролизе». Вл. Кистяковский.

---

1. Празднует в марте 1904 года восьмидесятый год от рождения.