БСЭ1/Линза

Линза
Большая советская энциклопедия (1-е издание)

Словник: Лилль — Маммалогия. Источник: т. XXXVII (1938): Лилль — Маммалогия, стлб. 38—42 ( РГБ )

ЛИНЗА (нем. Linse — чечевица), простейший оптический прибор, представляющий собой прозрачное для данного рода лучей тело, ограниченное двумя кривыми поверхностями (одна из поверхностей бывает иногда плоской).Рис. 1. Мнимое и действительное изображение. Материалом для Л. обыкновенно служит стекло, в виду чего иногда Л. называют также оптическими стеклами. Для ультрафиолетовых лучей стекло непрозрачно, а потому в этой области спектра пользуются кварцевыми и флюоритовыми Л. (предел прозрачности 1.850 и  — 1.250 Å). Для инфракрасных лучей с дли — а ной волны больше примерно 3 μ, сильно поглощаемых стеклом, пригодны кварц, флюорит(прозрачны до 3,5 и 9 μ) и в особенности каменная соль (до 16 μ).

Форма поверхностей, ограничивающих линзу, в большинстве случаев делается сферической, несмотря на то, что линза с такой формой поверхностей не может дать вполне резкого изображения (см. Аберрация). Преимущество поверхностей сферической формы состоит в легкости их шлифовки при изготовлении Л. Прямая, проходящая через центры кривизны сферических поверхностей, ограничивающих Л., называется оптической осью Л.; точки пересечения ее с поверхностями Л. называются вершинами; расстояние между вершинами называется толщиной Л. Если на Л., лишенную погрешности (см. Оптические приборы), падает пучок лучей, расходящихся из одной точки $A$, то после преломления угол расхождения изменяется. При этом лучи могут сделаться сходящимися, и в таком случае они пересекаются также в одной точке (рис. 1a); или же они могут оставаться расходящимися, и в таком случае их продолжения будут пересекаться в одной точке (рис. 1b) (см. Изображение оптическое). В первом Рис. 2.случае точка $A'$ пересечения преломленных лучей является действительным изображением точки $A$; во втором — точка $A'$ пересечения продолжений преломленных лучей называется мнимым изображением точки $A$. При падении на Л. пучка лучей, параллельных оптической оси, преломленные лучи пересекаются в одной точке (рис. 2a) или кажутся исходящими из одной точки (рис. 2b), называемой главным фокусом. Л. обладает двумя главными фокусами, соответствующими двум противоположным направлениям падающих лучей. Л., обладающие действительным главным фокусом, называются собирающими, Л., обладающие мнимым главным фокусом, называются рассеивающими.

Л. делятся в зависимости от своей толщины на тонкие и толстые. Л. считается тонкой, если ее толщина мала по сравнению с радиусами кривизны поверхностей. Расстояние от тонкой линзы до главного фокуса называется фокусным расстоянием и считается положительным, если направление этого отрезка совпадает с направлением световых лучей. Таким образом, собирающие Л. обладают положительным фокусным расстоянием, а рассеивающие — отрицательным. Если по обе стороны Л. находятся различные среды, то два фокусных расстояния Л. относятся, как показатели преломления этих сред. Для тонкой Л. в воздухе фокусное расстояние определяется формулой:

$f'={\frac {r_{1}r_{2}}{(n-1)(r_{1}-r_{2}}},$

(1)

‎где $n$ — показатель преломленияРис. 3. Линзы собирательные: a — двояковыпуклая, b — плосковыпуклая, c — выпукло-вогнутая (положительный мениск). Линзы рассеивающие: d — двояковогнутая, e — плосковогнутая, f — вогнуто-выпуклая (отрицательный мениск). вещества Л., $r_{1},r_{2}$ — радиусы кривизны первой и второй поверхностей Л. Радиусы кривизны отсчитываются от поверхностей к центрам кривизны и считаются положительными, если их направление совпадает с направлением световых лучей. Из формулы (1) следует, что к собирающим Л. принадлежат двояковыпуклая, плосковыпуклая и выпукло-вогнутая (т. н. положительный мениск, у которого кривизна выпуклой поверхности больше, чем вогнутой). К рассеивающим Л. относятся двояковогнутая, плосковогнутая и вогнуто-выпуклая (отрицательный мениск, у к-рого кривизна вогнутой поверхности больше, чем выпуклой) (рис. 3). Фокусное расстояние толстой Л. определяется следующей формулой:

$f'={\frac {nr_{1}r_{2}}{(n-1)[n(r_{1}-r_{2})+d(n-1)]}},$

(2)

‎$d$ — толщина Л.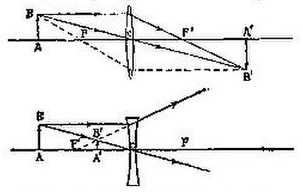Рис. 4. Построение изображений, даваемых тонкими линзами. При $d=0$ формула (2), очевидно, переходит в формулу (1) для тонкой Л. Из формулы (2) следует, что при изменении толщины Л. может измениться даже знак, т. е. Л. может из собирающей превратиться в рассеивающую и наоборот. — Л. характеризуются оптической силой, равной величине, обратной фокусному расстоянию. Оптическая сила Л. измеряется в диоптриях. Одна диоптрия соответствует оптической силе Л. с фокусным расстоянием, равным 1 м. Собирающие Л. обладают положительной оптической силой, рассеивающие — отрицательной. С ростом показателя преломления вещества Л. растет абсолютная величина оптической силы Л. — Если на оси линзы (рис. 4) находится предмет $AB$, Рис. 5. Главные плоскости различных линз.

‎то его изображение будет $A'B'$, причем расстояния $CA=s$ и $CA'=s'$ связаны между собой формулой Л.

${\frac {f}{s}}+{\frac {f'}{s'}}=1,$

(3)

‎где $f$ и $f'$ — расстояния от Л. до главных фокусов. Для Л., окруженных с обеих сторон однородной средой,

$f=-f'$ и ${\frac {1}{s'}}={\frac {1}{s}}+{\frac {1}{f'}}.$

(4)

Из формулы (3) легко может быть получена формула линзы Ньютона:

$xx'=ff',$

(5)

‎где

$x=FA=s-f$ и $x'=F'A'=s'-f',$

‎т. е. расстояния от предмета и изображения до соответствующих фокусов. Из формул (4 и 5) следует, что при приближении предмета из бесконечности к главному фокусу Л. изображение удаляется от второго фокуса в бесконечность. Если предмет лежит ближе главного фокуса к Л., то собирающая Л. дает мнимое изображение. Рассеивающая Л. всегда дает мнимое изображение. Из соображений симметрии следует, что плоский предмет, перпендикулярный оси Л., дает изображение, также перпендикулярное оси Л. Ход лучей в толстых Л. сложнее и зависит от расположения двух главных плоскостей, характеризующих систему Л. (рис. 5) (см. Оптические приборы).

Основное свойство главных плоскостей, используемое при построении изображений в толстых Л., состоит в том, что если луч, исходящий из предмета, пересекает одну главную плоскость $H$ на определенном расстоянии от оси, то сопряженный ему преломленный луч пересекает вторую главную плоскость $H$ на том же расстоянии от оси. Построение изображения в толстых Л. аналогично описанному выше построению для тонких Л. Отличие состоит в том, что у тонких Л. главные плоскости сливаются в одну (плоскость Л.), а в случае толстой Л. они раздвинуты и смещены по отношению к Л. (рис. 6). Приведенные выше формулы Л. справедливы и для толстой Л., только фокусные расстояния отсчитываются от главных плоскостей.

Все изложенное выше относится к Л., лишенным недостатков и обеспечивающим, следовательно,Рис. 6. Построение изображений, даваемых толстыми линзами. резкое изображение точки в виде точки (стигматическое изображение). Простая сферическая Л. дает резкое изображение только для лучей, лежащих в области, близкой к оси линзы (параксиальная, Гауссова область). Широкий пучок лучей, исходящий из точки, лежащей на оси линзы, не сводится опять в одну точку. Этот недостаток изображения называется сферической аберрацией (см.).

Другие недостатки изображений, даваемых Л., связаны со смещением светящейся точки с оси Л. и вызваны возникающей асимметрией в прохождении световых лучей (см. Астигматизм, Кома). В результате этих недостатков простая Л. может давать удовлетворительные изображения только при весьма малом действующем отверстии и небольших углах зрения. Также весьма серьезным недостатком простой Л. является наличие хроматической аберрации (см.), т. е. фокусирование на разных расстояниях лучей с различными длинами волн (различного цвета). Все перечисленные недостатки сильно ограничивают область применения простых Л. В большинстве оптических приборов применяются системы Л. подобранных так,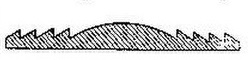Рис. 7. Линза Френеля. чтобы по возможности скомпенсировать ошибки отдельных Л. (см. Оптические приборы, Объектив). Наибольшее применение имеют отдельные линзы в очках (см.). Простые сферические линзы применяются также в качестве луп при небольших увеличениях (см. Лупа). Цилиндрические Л. применяются как для освещения узких щелей в качестве конденсоров, так и наоборот — для рассеивания лучей в посадочных авиационных прожекторах (см. Прожекторы). На маяках и в сигнальных аппаратах (светофорах) широкое применение нашли ступенчатые линзы Френеля (см. Маяки, Светофоры). Линза Френеля изображена на рисунке 7. Преимущества линз Френеля состоят в значительном уменьшении веса линз и устранении сферической аберрации. Особым и весьма важным типом Л. являются Л. с неоднородным показателем преломления. К числу таких Л. принадлежит хрусталик глаза человека и животных.

Электрические и магнитные Л., служащие для фокусировки электронных пучков в электронном микроскопе, катодных осциллографах, телевизорах и других приборах, аналогичны линзам с неоднородным показателем преломления. Самая простая электрическая линза представляет собой металлическую круглую диафрагму, обладающую либо положительным либо отрицательным потенциалом по отношению к катоду, испускающему электроны. Неоднородное электрическое поле вблизи диафрагмы искривляет пути электронов, чем и объясняется действие электрической Л. Приближенная формула для фокусного расстояния электрической Л.:

${\frac {1}{f}}={\frac {E_{2}-E_{1}}{4V}}$

‎где $E_{1},$ $E_{2}$ — градиенты поля до и после диафрагмы, $V$ — потенциал диафрагмы по отношению к катоду, из к-рого вылетают электроны. Когда $E_{1}<E_{2}$ Л. — собирающая, при $E_{1}>E_{2}$ Л. — рассеивающая. Магнитная Л. представляет собой соленоид, причем пучок электронов направлен вдоль оси соленоида. В магнитном поле линзы электроны двигаются по спиральным путям. Фокусное расстояние магнитной Л. обратно-пропорционально квадрату силы тока в обмотке соленоида. Электрические и магнитные линзы обладают такими же недостатками, что и обычные линзы, поэтому применяются системы линз.

Лит.: Справочная книга оптико-механика, ч. 1, М. — Л., 1936; Игнатовский В. С., Элементарные основы теории оптических приборов, Л. — М., 1933; Тудоровский А. И., Основания общей теории оптических приборов, Л., 1932; Берек М., Основы практической оптики, пер. с нем., М. — Л., 1933; Рор [М.], Оптические приборы, Л. — М., 1933; Шротт П., Практическая оптика, М. — Л., 1932; Вуд Р. В., Физическая оптика, М. — Л., 1936; Brüche H. und Scherzer О., Gеоmetrische Elektronenoptik, В., 1934.