БСЭ1/Колебания

Колебания
Большая советская энциклопедия (1-е издание)

Словник: Классы — Конкуренция. Источник: т. XXXIII (1938): Классы — Конкуренция, стлб. 310—321 ( РГБ )

КОЛЕБАНИЯ, процессы, при к-рых все состояния многократно повторяются (или приблизительно повторяются) со временем. Например: механические К., при к-рых через некоторые промежутки времени колеблющееся тело возвращается в одно и то же положение и приобретает снова одни и те же скорости; электрические К., при к-рых через некоторые промежутки времени повторяются те же самые значения напряжений и сил токов в цепи. Даже весьма различные по своей природе колебательные процессы (напр. механические и электрические) имеют между собой столь много общего, что оказывается возможным развить общую теорию колебательных явлений независимо от их природы; результаты этой теории в одинаковой мере приложимы как к механическим, так и к электрическим или смешанным электромеханич. К. или колебаниям еще каких-либо других типов.

Колебательные явления играют очень существенную роль в технике. В одних случаях колебательными явлениями пользуются для заранее определенных целей, и поэтому возникают вопросы создания К., их передачи и воздействия на различные системы. Так ставятся задачи в радиотехнике, акустике, отчасти электротехнике и т. д. В других случаях колебательные явления возникают помимо нашего желания и играют вредную роль: часто наблюдаются нежелательные и опасные К. сооружений, вибрации механизмов и т. д. Тогда возникают вопросы подавления этих К. или оценки их возможного вредного влияния. Так ставятся задачи в теории сооружений, в различных отраслях машиностроения и т. д. Но как в тех, так и в других случаях успешному разрешению задач очень существенно помогает глубокая аналогия между колебательными процессами в различных механич. и электрич. системах и общность методов трактовки колебательных проблем. — Общей чертой всех колебательных процессов, как уже указано, является их повторяемость; поэтому для характеристики К. пользуются теми их чертами, к-рые непосредственно связаны с повторяемостью процесса. Так, напр., одной из наиболее существенных характеристик К. служит указание того промежутка времени, в течение к-рого процесс повторяется или приблизительно повторяется. В тех случаях, когда всякое состояние системы точно повторяется через определенные и всегда одинаковые промежутки времени, К. называются периодическими, а величина этого промежутка времени — периодом К. Другие характеристики, применяемые для описания К., — размахи (в простейших случаях — амплитуды) К. и моменты прохождения процесса через определенное состояние (в простейших случаях — фаза К.) — также тесно связаны с повторяемостью самого процесса. Для решения вопросов, возникающих при изучении колебательных явлений, обычно бывает достаточно знать только эти характеристики процессов.

Вопросы, возникающие при изучении колебательных явлений, можно разделить на три основных группы: 1) вопросы, связанные с механизмом возбуждения К., 2) вопросы распространения К. в различных средах и 3) вопросы воздействия К. на различные физич. устройства. Вопросы второй группы обычно рассматриваются отдельно и составляют предмет учения о волнах. К собственно «теории колебаний» относят только первую и третью группы вопросов. В данной статье рассматривается гл. обр. только первая группа вопросов и лишь кратко — вопросы третьей группы, т. к. эти вопросы относятся уже к проблеме резонанса (см.). — Проблема возбуждения К. сводится к вопросу о том, при каких условиях могут происходить колебательные процессы в устройствах, не подвергающихся колебательным воздействиям извне; такие системы называются автономными. Действительно, если бы К. в рассматриваемом устройстве являлись результатом колебательного воздействия извне, то проблема возникновения К. не была бы решена, а лишь обойдена, т. к. остался бы нерешенным вопрос о способах создания воздействия.

Рассмотрим простейший случай возникновения К. в такой автономной системе. Представим себе массу $m$, подвешенную на пружине $S$ (рис. 1) (для упрощения рассуждений не будем принимать во внимание силы тяжести).Рис. 1 Если отклонить массу от положения равновесия в вертикальном направлении или сообщить ей в том же направлении начальную скорость, то масса $m$ будет двигаться то вверх то вниз, многократно проходя через положение равновесия, т. е. масса $m$ будет совершать колебания. Такие колебания называют свободными. Если бы в этой модели отсутствовали сопротивление воздуха и трение внутри самой пружины, а крепление пружины в точке а было бы абсолютно жестким, то в рассматриваемом устройстве не происходило бы потерь энергии, и груз совершал бы свои К. как угодно долго, не уменьшая размахов. К. происходили бы за счет того начального запаса энергии, которым обладала система в виде потенциальной энергии растянутой пружины или кинетической энергии груза, обладающего начальной скоростью. При колебаниях в такой системе происходят попеременно превращения потенциальной энергии в кинетическую и обратно.

Пока отклонения груза, а, значит, и растяжения пружины не очень велики, силу, с к-рой действует растянутая или сжатая пружина на груз, можно считать пропорциональной растяжению, т. е. положить $F=-kx$. Тогда уравнение движения массы $m$ по второму закону Ньютона напишется след. обр.:

$m{\frac {d^{2}x}{dt^{2}}}=-kx$

Решением этого уравнения являются гармонические функции sinus или cosinus.

Масса $m$ будет совершать т. н. гармонические, или синусоидальные, К., т. е. отклонения массы от положения равновесия будут выражаться так:

$x=A\sin(\omega _{0}t+\varphi )$

(1)

Здесь $A$ — наибольшее смещение массы, или амплитуда смещений; $\omega _{0}$ — число К., к-рое совершит масса за $2\pi$ секунд, или угловая частота К. (она связана с «обычной» частотой $f$, т. е. с числом К. в одну секунду, и с периодом $T$, т. е. с продолжительностью одного К., соотношением: $\omega _{0}=2\pi f={\frac {2\pi }{T}}$); $\varphi$ — начальная фаза К. Три величины — $A$, $\omega _{0}$ и $\varphi$ — характеризуют гармонические К. Из них одна $\omega _{0}$ зависит от свойств системы — массы груза $m$ и коэффициента упругости $k$ — и определяется соотношением: $\omega _{0}^{2}={\frac {k}{m}}$.Рис. 2 Две других величины, $A$ и $\varphi$, не зависят от свойств системы и определяются начальными условиями: $A$ — начальным отклонением и начальной скоростью, а $\varphi$ — началом отсчета времени. Таким образом, $\omega _{0}$ не зависит от $A$; это значит, что рассматриваемое нами устройство может совершать К. с любой амплитудой при неизменной частоте К. (изохронизм). Эту свойственную самому устройству частоту К. принято называть собственной частотой системы. Соответственный период есть собственный период системы. Изохронизм в рассматриваемом устройстве обусловлен тем, что силы, а значит и ускорения, пропорциональны смещениям.

Подобные же К., но, конечно, не механические, а электрические, могут происходить в электрическом контуре, составленном из емкости и катушки самоиндукции (рис. 2) (причем заряд на конденсаторе будет соответствовать смещению груза, а сила тока в цепи — скорости груза). Для того чтобы вызвать электрич. К. в таком контуре, надо сообщить конденсатору начальный заряд или в катушке контура возбудить ток. При этом индуктивность катушки $L$ будет играть такую же роль, как масса $m$, а емкость $C$ — такую, как ${\frac {1}{k}}$ — «податливость» пружины (величина, обратная упругости пружины). Подобно тому как в первом случае считалось, что пружина подчиняется закону Гука, т. е. что коэффициент упругости пружины есть величина постоянная, и здесь предполагается, что емкость конденсатора постоянна (напряжение на конденсаторе пропорционально заряду) и индуктивность катушки также постоянна (второму предположению в механич. модели соответствует предположение, что масса груза постоянна; при этом условии электродвижущая сила самоиндукции пропорциональна скорости изменения силы тока). Наконец, предположению об отсутствии сопротивления движению груза здесь соответствует предположение об отсутствии электрич. сопротивления в контуре. При этих допущениях получается вывод, что в контуре могут происходить гармонич. К. с собственной частотой ($\omega _{0}$ (определяемой соотношением $\omega _{0}^{2}={\frac {1}{LC}}$ — формула Томсона) и любой амплитудой, определяемой только начальными условиями. В обоих упомянутых случаях К. предполагалось, что упругости и массы или емкости и самоиндукции постоянны, а это приводит к тому, что дифференциальные уравнения, описывающие поведение рассматриваемой системы, оказываются линейными. Этот термин принято распространять и на самые колебательные устройства. Однако предположения о том, что свойства системы не зависят от происходящих в ней процессов, не всегда соблюдаются. В большей или меньшей степени эта зависимость всегда имеет место; напр., закон Гука справедлив только при не слишком больших удлинениях пружины. В специальных случаях эта зависимость может, быть весьма значительна, напр. индуктивность катушки с железным сердечником очень сильно зависит от силы протекающего по ней тока. При рассмотрении поведения систем, обладающих такими свойствами, приходят к нелинейным дифференциальным уравнениям; поэтому и рассматриваемые устройства называются нелинейными. В какой степени учет указанных усложнений является необходимым, зависит не только от свойств самой системы, но и от того, какие поставлены вопросы. В зависимости от этого одно и то же устройство можно рассматривать либо как систему нелинейную, либо как линейную. В нелинейных системах также могут происходить К., но уже несинусоидальной формы. К таким несинусоидальным К. уже неприменимы, строго говоря, понятия амплитуды и фазы, введенные нами для гармония. К. Однако и в случае негармонич. К. принято говорить об амплитуде К., понимая под этим наибольшие размахи К. В нелинейной системе без трения амплитуда К. (так же, как и в линейной) зависит от начальных условий; частота же К. зависит не только от свойств системы, но и от амплитуд К., т. е. изохронизм не имеет места. Это обусловлено как-раз тем, что самые свойства системы зависят от происходящих в ней процессов. Таким образом, понятие собственной частоты системы в нелинейных системах теряет смысл. — Если в нелинейных системах отсутствуют потери энергии, то снова получаются стационарные К. с постоянной амплитудой. Системы, в к-рых не происходит потерь энергии, принято называть консервативными (см. Консервативная система сил). Следовательно, в консервативных системах, независимо от того, рассматривают ли их как линейные или как нелинейные, могут происходить стационарные К. с любой амплитудой, определяемой начальными условиями.

Однако в реальных физич. устройствах всегда действуют силы, имеющие характер трения и вызывающие потери энергии.Рис. 3 Такие системы, в которых происходят потери энергии, называются диссипативными. Очевидно, что в диссипативных системах начальный запас энергии, сообщенный системе, убывает при К., и, значит, амплитуды К. должны убывать, т. е. К. должны быть затухающими (в отличие от этого, стационарные К. часто называют незатухающими). Характер затухания К. зависит от характера сил, вызывающих потери энергии. Простейший случай представляют механич. системы с силой трения, пропорциональной скорости, или электрич. контуры с постоянным электрич. сопротивлением; затухание при этом происходит по показательному закону. Рассмотрим электрический контур, который, кроме емкости $C$ и индуктивности $L$, обладает еще постоянным сопротивлением $R$ (рис. 3).

Этот контур, поскольку почти вся его емкость сосредоточена в конденсаторе, можно рассматривать как квазистационарный и применять к нему законы Кирхгофа. В отсутствии внешних электродвижущих сил в контуре существует только электродвижущая сила самоиндукции $-L{\frac {di}{dt}}$ или $-L{\frac {d^{2}q}{dt^{2}}}$, если $i$ — сила тока в контуре, а $q$ — заряд на обкладках конденсатора. С другой стороны, в контуре существуют падения напряжения на сопротивлении $=R{\frac {dq}{dt}}$ и на конденсаторе $={\frac {q}{c}}$. Следовательно, по второму закону Кирхгофа $-L{\frac {d^{2}}{dt^{2}}}=R{\frac {dq}{dt}}+{\frac {q}{c}}$ или ${\frac {d^{2}q}{dt^{2}}}+2h{\frac {dq}{dt}}+\omega _{0}^{2}q=0$, где $h={\frac {R}{2L}}$ и $\omega _{0}={\frac {1}{\sqrt {LC}}}$. Решением этого уравнения служат показательные функции вида $A\mathrm {e} ^{kt}$, где $k$ — корень характеристического уравнения:

$k^{2}+2hk+\omega _{0}^{2}=0$.

В том случае, когда $h^{2}<\omega _{0}^{2}$, т. е. $\left({\frac {R}{2L}}\right)^{2}<{\frac {1}{LC}}$ уравнение имеет два комплексных сопряженных корня $k_{1,2}=-h\pm i\omega _{1}$, где $\omega _{1}={\sqrt {\omega _{0}^{2}-h^{2}}}$, и полное решение исходного уравнения имеет вид:

$q=A\mathrm {e} ^{(-h+i\omega _{1})t}+B\mathrm {e} ^{(-h-i\omega _{1})t}$.

Пользуясь формулой Эйлера для перехода от показательных функций с мнимым показателем к гармоническим функциям, можно привести решение к виду:

$q=A_{0}\mathrm {e} ^{-{\frac {R}{2L}}t}\sin {(\omega _{1}t+\varphi )}$,

(2)

где $\omega _{1}$ попрежнему определяется свойствами системы и выражается так:

$\omega _{1}={\sqrt {{\frac {1}{LC}}-{\frac {R^{2}}{4L^{2}}}}}$.

Две других величины, $A_{0}$ (начальный заряд) и $\varphi$ — начальная фаза, определяются, как и прежде, начальными условиями.

В том случае, когда сопротивление контура не слишком велико, изменение заряда на обкладках конденсатора и изменения силы тока в цепи будут носить также колебательный характер, мало отличный от синусоидального. При большем сопротивлении К. очень далеки от периодических, и понятие периода по отношению к таким К. уже совсем неприменимо. Когда же сопротивление очень велико, в системе вообще уже не могут возникать К., и начальные отклонения затухают апериодически, т. е. спадают до ноля (без многократного прохождения через состояние равновесия). В этом случае системы называются апериодическими; системы же с малым сопротивлением, в к-рых могут происходить К., называются колебательными.

Действительно, если $\left({\frac {R}{2L}}\right)^{2}$ гораздо меньше ${\frac {1}{LC}}$ или ${\frac {R}{2}}{\sqrt {\frac {C}{L}}}\ll 1$, то приблизительно процесс повторяется. За время $T_{1}=2\pi :$ ${\sqrt {{\frac {1}{LC}}-{\frac {R^{2}}{4L^{2}}}}}\approx 2\pi {\sqrt {LC}}$ синус вернется к прежнему значению, а функция $\mathrm {e} ^{-{\frac {R}{2L}}t}$ очень мало изменит свое значение — она уменьшится в $\mathrm {e} ^{-d}$ раз, где $d={\frac {R}{2l}}\cdot T_{1}\cong {\frac {R}{2L}}\cdot 2\pi {\sqrt {LC}}=\pi R{\sqrt {\frac {C}{L}}}$ (3); но по нашему предположению $R\cdot {\sqrt {\frac {C}{L}}}\ll 1$, следовательно, и $d$ гораздо меньше $1$ и $\mathrm {e} ^{-d}$ близко к единице. Следовательно, при достаточно малых $R$ будут происходить К., мало отличающиеся от синусоидальных. Различие это будет заключаться в том, что амплитуды К. не будут оставаться постоянными, а будут уменьшаться (рис. 4), образуя убывающую геометрическую прогрессию: отношение двух соседних амплитуд равно $\mathrm {e} ^{d}$, а натуральный логарифм этого отношения равен $d$. Поэтому $d$ носит название логарифмического декремента затухания. Чем больше $R$, тем быстрее затухают К., вместе с тем они становятся все меньше и меньше похожими на периодические. Пока $R$ мало и К. еще мало отличаются от периодических, можно, хотя и не вполне строго, применять к ним термин «период»; этот «псевдопериод» $T_{1}={\frac {2\pi }{\sqrt {{\frac {1}{LC}}-{\frac {R^{2}}{4L^{2}}}}}}$ при малых В близок к собственному периоду контура $T=2\pi {\sqrt {LC}}$.

Когда сопротивление контура столь велико, что $h^{2}>\omega _{0}^{2}$, процессы в контуре вовсе не имеют колебательного характера. В этом случае корни характеристич. уравнения оказываются оба действительными, и процессы в контуре описываются линейной комбинацией двух показательных функций:

$q=A\mathrm {e} ^{k_{1}t}+B\mathrm {e} ^{k_{2}t}$.

При любых значениях постоянных $A$ и $B$, т. е. при любых начальных условиях, $q$ не может больше одного раза пройти через ноль и в дальнейшем приближается к нолю асимптотически.

В том случае, когда сопротивление контура уже нельзя считать постоянным (точнее,Рис. 4 когда в контуре есть проводники, не подчиняющиеся закону Ома, напр., газовая разрядная трубка), линейность системы будет нарушена. Вместе с тем изменится и закон затухания К. — амплитуды будут убывать уже не по показательному закону, а как-то иначе. Но пока система остается диссипативной, т. е. пока все проводники обладают такими свойствами, что прохождение по ним тока связано с потерей энергии, К. всегда будут затухать и, следовательно, стационарные К. в диссипативных системах, как линейных, так и нелинейных, невозможны.

Между тем для техники имеют очень большое значение и для физики представляют особый интерес именно стационарные (незатухающие) К. Достаточно указать на то, что вся современная радиотехника пользуется только незатухающими К. Поэтому проблема возбуждения и поддержания стационарных К. уже давно привлекла внимание физиков и техников. Из сказанного ранее сразу видно, в каком направлении следует искать решения проблемы поддержания стационарных К. Причиной затухания К. являются потери энергии, обусловленные наличием сил, подобных силам трения. Силы этого типа существуют во всякой реальной системе, и устранить их невозможно. Впрочем, даже если бы их и удалось устранить, это не было бы решением вопроса, ибо нас интересуют такие источники стационарных К., к-рые способны отдавать энергию различным потребителям, т. е. в которых стационарные К. происходят, несмотря на наличие потерь и отдачу энергии. Следовательно, решение проблемы возбуждения стационарных К. следует искать не в устранении потерь энергии, а в компенсации их за счет какого-либо специального источника энергии. Можно было бы попытаться осуществить такое устройство, в котором обеспечена компенсация потерь энергии в каждый отдельный элемент времени, т. е., чтобы в каждый элемент времени в систему из источника поступало в точности столько же энергии, сколько расходуется в самой системе. Однако осуществить компенсацию потерь энергии оказывается возможным только в среднем за период; в связи с этим системы, создающие стационарные К., приобретают черты, существенно отличающие их от консервативных систем. Это различие заключается прежде всего в том, что компенсация потерь энергии в среднем за период происходит не при любых, а только при каких-то определенных амплитудах К. Поэтому интересующие нас устройства могут создавать стационарные К. не произвольной, а вполне определенной амплитуды, не зависящей, вообще говоря, от начальных условий и определяемой свойствами самого устройства. Начальные условия играют роль только в вопросе возникновения К., от них зависит ход установления К., а иногда и самая возможность возникновения стационарных К. Стационарные К. происходят в таких системах не за счет начального запаса энергии (как это имеет место в консервативных системах), а за счет систематич. поступления энергии из какого-либо источника энергии. Такие колебания носят название автоколебаний. Устройства, способные создавать автоколебания, называются автоколебательными системами.

Всякое автоколебательное устройство должно, очевидно, обладать, во-первых, резервуаром энергии, из к-рого черпается энергия для компенсации потерь, и, во-вторых, каким-то механизмом, регулирующим поступление энергии из резервуара таким образом, чтобы за период в систему поступало бы как-раз нужное количество энергии. Этот механизм не только определяет количество поступающей из резервуара энергии, но и обеспечивает поступление этой энергии в нужном темпе. Типичными примерами автоколебательных устройств могут служить среди механич. систем часы, а среди электрических — ламповый генератор, применяемый в радиотехнике для создания К. высокой частоты. И в том и в другом из автоколебательных устройств легко выделить названные нами основные элементы: в часах резервуаром энергии служит заведенная пружина или поднятая гиря, а механизмом, регулирующим поступление энергии к колеблющемуся маятнику, — т. н. храповое устройство, передающее маятнику толчки от заведенной пружины в те моменты, когда маятник проходит через определенные положения. В ламповом генераторе, схема которого приведена на рис. 5, источником энергии служит анодная батарея Б, а регулирующим механизмом — электронная лампа, включенная по схеме обратной связи, т. е. со связью между цепью сетки и цепью анода.Рис. 5 В схеме, приведенной на рис. 5, эта связь осуществляется индуктивно из-за наличия взаимоиндукций $M$ между катушками $L$ и $L_{1}$ Благодаря обратной связи энергия из анодной цепи (поставляемая анодной батареей) может поступать в колебательный контур $LC$, включенный в цепь сетки. Для колебательного контура, включенного по схеме обратной связи, можно, пользуясь вторым законом Кирхгофа, составить уравнение, подобное тому, которое было составлено выше для обычного колебательного контура. Различие будет состоять лишь в том, что помимо электродвижущей силы самоиндукции, в контуре, благодаря обратной связи, будет еще индуцироваться электродвижущая сила, обусловленная изменениями анодного тока. Таким образом, уравнение для колебательного контура $LC$, включенного по схеме рис. 5, будет иметь вид:

$LC{\frac {d^{2}v}{dt^{2}}}+RC{\frac {dv}{dt}}+v=M{\frac {dJ_{a}}{dt}}$

(4)

(в этом случае удобнее в качестве независимой переменной выбрать не заряд $q$, a $v={\frac {q}{c}}$, т. е. напряжение на обкладках конденсатора). Далее мы должны принять во внимание, что $J_{a}$ есть некоторая функция от напряжений на сетке и аноде ламп. Для упрощения мы будем считать, что электродвижущие силы на анодной катушке $L_{1}$ малы по сравнению с напряжением батареи Б и что поэтому напряжение на аноде лампы можно даже при наличии К. в контуре считать практически постоянным. Тогда сила анодного тока есть функция только от напряжения на сетке $V_{g}$ или в нашей схеме от напряжения $v$ на обкладках конденсатора. Зависимость $J_{a}$ от напряжения на сетке всегда нелинейна уже по одному тому, что ток в лампе может течь только в одну сторону и что существует насыщение, т. е. как при уменьшении, так и при увеличении сеточного напряжения мы всегда в конце концов попадаем в области, где сила тока вообще не изменяется при изменении напряжения. Зависимость $J_{a}$ от $V_{g}$ обычно задается графически в виде т. н. характеристики анодного тока. Типичная характеристика приведена на рис. 6. Итак, мы можем написать

${\frac {d^{2}v}{dt^{2}}}+{\frac {R}{L}}{\frac {dv}{dt}}+\omega _{0}^{2}v={\frac {M}{LC}}\varphi '(v){\frac {dv}{dt}}$,

(5)

где функция $\varphi (v)$ выражает зависимость $J_{a}$ от $v$. В некоторых пределах ее всегда можно задать аналитически. Мы можем привести уравнение (5) к виду

${\frac {d^{2}v}{dt^{2}}}+{\frac {RC-MS}{LC}}{\frac {dv}{dt}}+\omega _{0}^{2}v=0$,

(6)

где $S=\varphi '(v)={\frac {d\varphi }{dv}}$ есть крутизна характеристики лампы (см. Электронная лампа).

Так как крутизна характеристики есть величина переменная, зависящая от $v$, то полученное нами уравнение нелинейно. Общих методов для решения нелинейных дифференциальных уравнений, как известно, не существует. Для полученного нами уравнения при нек-рых существенных ограничениях могут быть найдены приближенные решения. Именно, если сопротивление $R$ контура достаточно мало, приближенное решение уравнения (6) есть гармонии, функция с угловой частотой $\omega _{0}$, но уже не с произвольной, а с вполне определенной амплитудой (или одной из нескольких вполне определенных амплитуд), зависящей не от начальных условий, а от параметров самой системы.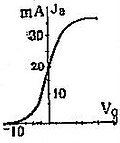Рис. 6 Но для того, чтобы такое решение было возможно, коэффициент взаимной индуктивности $M$ должен быть определенного знака и больше некоторого критич. значения, т. е. обратная связь должна быть определенного направления и достаточно сильной. Этот результат легко поддается физич. истолкованию с точки зрения баланса энергии в системе. В течение нек-рой части периода (когда $MS>RC$) в контур может поступать больше энергии, чем за это время в нем теряется, т. е. контур в это время ведет себя так, как будто он обладает «отрицательным сопротивлением». В течение другой части периода (когда $MS<RC$) потери энергии в контуре больше, чем поступление энергии из анодной цепи, и контур ведет себя как обычный контур с положительным сопротивлением. И если в среднем за период (только в среднем за период, а не в каждый отдельный момент) сопротивление равно нолю, то в контуре происходят стационарные К. Значит, для того чтобы были возможны стационарные К., сопротивление системы должно изменяться; система должна обладать переменным сопротивлением, зависящим от ее состояния, значит, она должна быть нелинейной.

Этот вывод, сделанный нами на основании очень упрощенных и не строгих рассуждений для одного только частного случая, может быть строго обоснован и обобщен на все автоколебательные устройства. Для того чтобы система могла совершать стационарные К. с амплитудой, не зависящей от начальных условий, она должна обладать нелинейностью определенного типа в диссипативных членах, т. е. параметры системы, характеризующие потери энергии в ней, должны известным образом зависеть от состояния системы. В простейшем случае, как мы видели, это сводится к тому, что сопротивление системы в нек-рой области ее состояний должно становиться отрицательным. В обоих рассмотренных нами примерах автоколебательных систем, помимо источника энергии и регулирующего механизма, можно выделить еще одну часть — «собственно» колебательную систему. В часах этой системой является маятник, а в ламповом генераторе — колебательный контур $L_{1}C$. Наличие такой колебательной системы, способной в отсутствии источника энергии и регулирующего механизма совершать свободные затухающие колебания, не является обязательным для автоколебательных устройств. Существуют и такие автоколебательные устройства, в к-рых нет никаких частей, способных совершать свободные К. Но присутствие колебательной системы сообщает автоколебательному устройству некоторые весьма существенные и полезные в большинстве случаев черты и, в частности, позволяет легко получить близкие к синусоидальным К., а это часто бывает очень важно.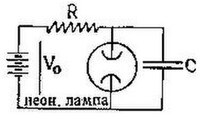Рис. 7Рис. 8 Период этих автоколебаний обычно близок к периоду свободных К., к-рые могут происходить в системе в отсутствии источника энергии и регулирующего механизма. Такие системы принято сейчас называть «томсоновскими», т. к. период их примерно определяется той же формулой Томсона, к-рой определяется период свободных К. в колебательном контуре. Системы же «не томсоновские», т. е. лишенные колебательных контуров, обычно совершают автоколебания, существенно отличные от синусоидальных. Период этих автоколебаний часто приближенно определяется т. н. временем релаксации (в механике временем релаксации называют время, характеризующее скорость исчезновения упругих деформаций в среде, обладающей большой вязкостью; по аналогии, в области электрич. явлений временем релаксации принято называть, напр., время, характеризующее скорость разряда конденсатора через сопротивление). Это дало повод называть К. такого типа «релаксационными». Типичным примером системы,, создающей релаксационные К. («релаксационной системы»), может служить схема с неоновой лампой (рис. 7). Характерная «пилообразная» форма колебаний, создаваемых этой схемой, приведена на рис. 8. Частота этих колебаний существенно зависит от режима схемы (величины $V_{0}$).

При неизменном режиме частота автоколебаний обратно пропорциональна произведению $RC$.

Рассматривая проблему возникновения К. в автономных системах, мы пока ограничивались только системами с одной степенью свободы. Но и по отношению к системам со многими степенями свободы, а также и системам с «распределенными параметрами» или сплошным системам справедливы все основные положения, высказанные выше, а именно: в консервативных системах возможны стационарные К., но с амплитудами, целиком зависящими от начальных условий. В диссипативных системах происходят только затухающие К., и стационарные К. невозможны. В нелинейных системах с нелинейностью определенного типа в членах, характеризующих рассеяние энергии в системе, возможны автоколебания, т. е. стационарные К. с амплитудой, не зависящей от начальных условий. Однако самый характер К., возникающих в системах со многими степенями свободы, может существенно отличаться от К. в системах с одной степенью свободы.

Рассмотрим в качестве примера систему с двумя степенями свободы, изображенную на рис. 9, т. е. две массы $m_{1}$ и $m_{2}$, укрепленные на пружинах. Эту систему удобно рассматривать, как две связанных системы. Однако для дальнейшего это не существенно, и все основные выводы, будут справедливы для всякой системы с двумя степенями свободы, а не только для таких устройств, к-рые можно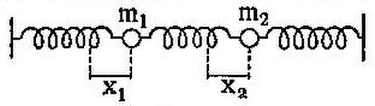Рис. 9 рассматривать как две связанные системы. Только нужно будет все сказанное относить не к координатам двух систем, а к двум координатам одной и той же системы. Ограничимся достаточно малыми отклонениями шариков $m_{1}$ и $m_{2}$ так, чтобы пружины можно было бы считать подчиняющимися закону Гука. Кроме того, положим для простоты, что оба шарика имеют одинаковую массу $m$ и все три пружины — одинаковую упругость $k$. Тогда для движения обоих шариков мы получим на основании второго закона Ньютона следующие уравнения:

$m{\frac {d^{2}x_{1}}{dt^{2}}}=-kx_{1}+k(x_{2}-x_{1})$ и $m{\frac {d^{2}x_{2}}{dt^{2}}}=-kx_{2}+k(x_{1}-x_{2})$

или $m{\frac {d^{2}x_{1}}{dt^{2}}}+2kx_{1}-kx_{2}=0$; $m{\frac {d^{2}x_{2}}{dt^{2}}}+2kx_{2}-kx_{1}=0$,

(7)

где $x_{1}$ и $x_{2}$ — смещения обоих шариков относительно положений равновесия. Общие решения этой системы уравнений имеют вид:

$x_{1}=A\cos {({\sqrt {\frac {k}{m}}}t+\varphi _{1})}+B\cos {({\sqrt {\frac {3k}{m}}}t+\varphi _{2})}$ $x_{2}=A\varkappa _{1}\cos {({\sqrt {\frac {k}{m}}}t+\varphi _{1})}+B\varkappa _{2}\cos {({\sqrt {\frac {3k}{m}}}t+\varphi _{2})}$,

где $\varkappa _{1}$ и $\varkappa _{2}$ — т. н. коэффициенты распределения, определяемые параметрами системы. Начальными условиями определяются только константы $A$ и $B$, а коэффициенты $\varkappa _{1}$ и $\varkappa _{2}$ определяются параметрами системы. Это значит, что начальными условиями мы можем, напр., задать любое распределение амплитуд обоих К. одного шарика, но тогда распределение амплитуд обоих К. другого шарика будет уже вполне определенным. При наличии начальных отклонений или начальных толчков оба шарика будут совершать К., но уже не гармонические, а более сложного характера. Каждый шарик совершает К., к-рые, вообще говоря, представляют собой сумму двух гармонич. К. с различными периодами. Как и в случае линейной системы, с одной степенью свободы, период этих К. определяется свойствами системы, а амплитуды и фазы: обоих К. — начальными условиями. Однако отношение амплитуд непроизвольно и определяется параметрами системы. В частности, можно выбрать начальные условия так, чтобы первый шарик совершал только одно из двух гармонич. К.; для этого достаточно оба шарика отклонить одинаково в одну сторону или в разные стороны. Тогда и второй шарик будет совершать только то же самое гармонии. К., которое совершает первый. Вообще же говоря, каждый шарик будет одновременно совершать оба гармонии. К. Эти гармонич. К., из к-рых состоит движение каждого из шариков, носят название

нормальных К. системы, а их частоты носят название нормальных частот.

В системе с двумя степенями свободы существуют, т. о., два нормальных К. Эти выводы легко распространить и на системы с числом степеней свободы больше двух. Число нормальных К. всякой системы равно числу степеней свободы этой системы. Если система имеет $n$ степеней свободы, то движение по каждой координате может быть представлено как сумма $n$ гармонич. К. с различными периодами, определяемыми параметрами системы, и амплитудами и фазами, определяемыми начальными условиями. Но если распределение амплитуд нормальных К. по одной из координат уже задано (начальными условиями), то распределение амплитуд этих же К. по остальным координатам задается свойствами самой системы. Если число степеней свободы системы очень велико, то этим можно воспользоваться для упрощения задачи. Так, например, в системе, состоящей из $N$ одинаковых шариков, соединенных пружинками (рис. 10), задача упрощается потому, что уравнение движения для всех шариков, кроме двух крайних, имеет совершенно одинаковый вид:

$m{\frac {d_{2}x_{i}}{dt^{2}}}=-kx_{i+1}+k(x_{i+1}-x_{i});i=1,2\dots N.$

(8)

Только для двух крайних шариков уравнения движения имеют иной вид, зависящий от тех условий, в к-рые поставлены крайние шарики. Из системы (8) для каждого $x$ получается решение в виде суммы $n$ гармонич. К. (нормальных К.), частоты к-рых определяются свойствами системы. Если число шариков велико и все шарики и пружинки одинаковы, то нормальные частоты приблизительно образуют ряд $\omega$, $2\omega$, $3\omega$ и т. д.

Величина амплитуды и фазы различных нормальных К. задаются попрежнему начальными условиями, а распределение амплитуд по различным шарикам — условиями, в к-рые поставлены крайние шарики^[1]. Если число шариков беспредельно возрастает, то как массы, так и упругость оказываются все более и более равномерно распределенными по системе, и система все большей больше приближается к сплошной системе или к системе с распределенными параметрами.Рис. 10 В пределе нашу систему из шариков и пружины мы можем рассматривать как — сплошной стержень, обладающий соответствующей массой и упругостью. Так, мы приходим к простейшей задаче о К. в сплошных системах. Вместо уравнения типа (8) для одного шарика мы получим в этом случае уравнение для бесконечно тонкого слоя, толщиной $dx$, вырезанного в перпендикулярном к оси стержня направлении. Но т. к. смещение слоев в этом случае непрерывно распределено по стержню, то его уже не следует относить к дискретным точкам, а можно рассматривать как непрерывную функцию координаты $x$. Упругие силы, зависящие от деформаций, определяются вторыми производными смещений по координатам, а так как смещения зависят также от времени (стержень колеблется), то для определения упругих сил в какой-либо момент нужно брать частные производные от смещений по координатам. С другой стороны, ускорение какой-либо точки выражается как вторая частная производная от смещения по времени. В конечном счете вместо $N$ уравнений (8) мы получим только одно уравнение, но в частных производных:

$\varrho {\frac {\partial ^{2}y}{\partial t^{2}}}=E{\frac {\partial ^{2}y}{\partial x^{2}}},$

(9)

где $\varrho$ — плотность, а $E$ — упругость в системе.

Это уравнение само по себе не определяет никаких собственных частот, а лишь скорость распространения возмущения по стержню. Но в ограниченном стержне возмущение через некоторое время должно отразиться от конца и вернуться назад. Поэтому краевые условия определяют период К. стержня и вместе с тем все нормальные частоты, к-рые в рассматриваемом случае однородного стержня будут точно кратными основной частоте К. Это т. н. гармонические обертоны (если бы стержень был неоднородным, то обертоны не были бы кратными основному тону, т. е. не были бы гармоническими). Форма К. стержня, т. е. амплитуды и фазы всех нормальных К., определяется начальными условиями. Рассмотренный нами случай продольных К. в упругом стержне является простейшей задачей о К. в сплошной системе. Однако основные черты этих К., установленные нами для этого простейшего случая, остаются справедливыми и для более сложных сплошных систем. Наличие нескольких степеней свободы может также и в автоколебательной системе изменить характер создаваемых этой системой автоколебаний. В этом случае в системе могут существовать, напр., сразу два близких к синусоидальным автоколебания различных периодов или К. еще более сложного состава.

Рассмотренными выше двумя типами К. (свободные К. и автоколебания) исчерпываются все случаи возникновения К. в автономных системах. Перейдем теперь к краткому обзору различных случаев возникновения К. в системах, подвергающихся колебательному внешнему воздействию, т. е. в системах неавтономных, а вместе с тем к рассмотрению третьей группы вопросов — о воздействии К. на различные устройства. К., к-рые происходят в неавтономных системах, естественно разделить на две части — на К., к-рые происходят независимо от колебательного внешнего воздействия и, следовательно, принадлежат к одному из рассмотренных выше типов, и на К., навязанные внешним воздействием. Однако такое разделение возможно только в линейных системах, к которым применим принцип суперпозиции (см.). Поэтому мы будем говорить только о линейных системах, а в отношении нелинейных систем ограничимся только самыми краткими замечаниями.

В линейных системах независимо от внешнего воздействия могут возникать только К., к-рые мы назвали выше собственными или свободными. Мы знаем уже, чем определяется период, амплитуда и фаза этих К. Рассмотрим поэтому только вопрос о периоде, амплитуде и фазе навязанных извне К. Внешнее колебательное воздействие чаще всего заключается в том, что на систему действует колебательная внешняя сила или каким-либо точкам системы навязывается извне заданное колебательное движение. Навязанные таким образом К. принято называть вынужденными К. Но возможен и другой тип внешнего колебательного воздействия, приводящий к возникновению К. в системе. Именно, воздействие может быть таково, что оно изменяет какой-либо параметр системы. Примером такого воздействия может служить периодическое изменение натяжения струны, применяемое в опыте Мельде. В случае такого параметрического воздействия при известных соотношениях между частотами воздействия и собственными частотами системы возбуждаются колебания, по своему характеру существенно отличающиеся от вынужденных. Эти колебания носят название параметрически-возбужденных.

Период вынужденных К. целиком определяется периодом внешнего воздействия. Амплитуда же вынужденных К. зависит не только от амплитуды внешнего воздействия (в рассматриваемых нами линейных системах амплитуда вынужденных К. пропорциональна амплитуде внешнего воздействия), но и от других факторов — от соотношения между частотами внешнего воздействия и частотой собственных К., а также от величины затухания собственных К. системы. При данном соотношении между частотами амплитуда вынужденных К. тем больше, чем меньше сопротивление. Более сложной является зависимость амплитуды вынужденных К. от соотношения между частотами. Если затухание собственных К. в системе невелико, то вблизи нек-рых соотношений между частотами внешнего воздействия и частотами собственных К. в системе амплитуда вынужденных К. резко возрастает, — наступают явления резонанса.

В простейшем случае линейной системы с одной степенью свободы, находящейся под действием гармонический внешней силы, явление резонанса наступает тогда, когда частота внешнего воздействия приближается к частоте собственных К. системы. При сближении этих двух частот амплитуда вынужденных К. быстро увеличивается, достигает максимума и затем снова убывает. При этом величина достигаемого максимума обратно пропорциональна затуханию собственных К. в системе. Поэтому в системах с малым затуханием амплитуды вынужденных К. при резонансе могут быть очень велики. Для того чтобы вынужденные К. успели установиться, нужно время тем большее, чем меньше затухание системы. Графически зависимость амплитуды установившихся вынужденных колебаний $X$ от соотношения частот собственной $n_{0}$ и внешнего воздействия $n$ изображена на рис. 11.Рис. 11 Кривые, которые выражают эту зависимость, носят название кривых резонанса. На рис. 11 приведены три кривые резонанса для трех разных значений логарифмич. декремента затухания собственных колебаний в контуре. Чем меньше декремент, тем больше соответствующая амплитуда вынужденных К. и тем выше проходит резонансная кривая. В области резонанса вместе с изменением амплитуды вынужденных К. происходят и резкие изменения фазы вынужденных колебаний по отношению к фазе внешнего воздействия. В том случае, когда на линейную систему действует не гармоническая, а какая-либо иная периодич. сила, резонанс наступает только при условии, если во внешнем воздействии содержится гармония. К., частота к-рого близка к частоте собственных К. в системе. Именно в силу этого свойства линейных систем как приемников (в качестве приемников К. мы чаще всего пользуемся линейными системами) приобретает особый физический интерес проблема разложения периодич. функций в ряд Фурье, т. е. на гармонические составляющие. Для того чтобы узнать результат периодического, но не гармонического воздействия на линейную систему, достаточно знать, какие именно гармонические составляющие содержит это воздействие. Определяя результат воздействия каждой гармонической составляющей в отдельности и пользуясь принципом суперпозиции, мы всегда сможем определить результат одновременного воздействия всех составляющих, т. е. рассматриваемого периодического воздействия.

В линейных системах со многими степенями свободы картина усложняется. Зависимость амплитуды вынужденных К. от частотных соотношений становится более сложной, и резонансные явления могут наступать не в одном, а в нескольких местах при нескольких различных частотах внешнего воздействия, соответствующих различным собственным частотам системы. Наконец, особенно сложными становятся все эти явления при системах нелинейных. Среди внешних воздействий на нелинейную систему особый интерес представляет случай внешнего воздействия на нелинейную систему, способную совершать автоколебания или близкую к этому. В этом случае при соблюдении нек-рых соотношений между частотами и нек-рых других условий наступают явления автопараметрического возбуждения.

Лит.: Тимошенко С. П., Теория колебаний в инженерном деле, М. — Л., 1931; Баркхаузен Г., Электронные лампы, т. II—III, M. — Л., 1932; Андронов А. А., Xайкин С. Э., Теория колебаний, ч. 1, М. — Л., 1937.

---

1. Эти условия носят название граничных или краевых условий. Простейшие краевые условия могут состоять, напр., в том, что крайние шарики свободны или закреплены неподвижно.