ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ, поверхности, образованные движением прямой линии (прямолинейной образующей) при скольжении ее по некоторой кривой (направляющей). Касательная плоскость к линейчатой поверхности содержит в себе всю прямолинейную образующую,
Рис. 1.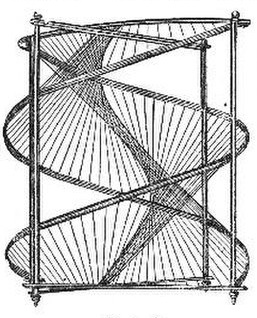
Рис. 2. проходящую через точку касания. Л. п. разделяются на развертывающиеся и косые. Модель развертывающейся Л. п. изображена на рис. 1, косой — на рис. 2. Л. п. называется развертывающейся, если любая ее часть может быть наложена на плоскость без складок и разрывов. Простейшими примерами таких поверхностей являются конусы и цилиндры. Все прямолинейные образующие развертывающейся Л. п. касаются нек-рой пространственной кривой (ребро возврата). На рис. 1 Л. п. образована касательными к винтовой линии, к-рая на модели показана сгущением натянутых нитей — образующих поверхности. В случае конуса ребро возврата вырождается в точку, а у цилиндра — в бесконечно-удаленную точку. Касательная плоскость к развертывающейся Л. п. во всех точках прямолинейной образующей одна и та же (т. е. она не будет вращаться, если перемещать точку касания вдоль прямолинейной образующей). Все касательные плоскости к развертывающейся Л. п. образуют семейство плоскостей, зависящее от одного параметра. Неразвертывающаяся Л. п. называется «косой». Простейшими примерами косых Л. п. могут служить однополостный гиперболоид и гиперболический параболоид (см.). Касательные плоскости к косой Л. п. в различных точках одной и той же прямолинейной образующей различны (если перемещать точку касания вдоль прямолинейной образующей, то касательная плоскость будет вращаться вокруг этой прямолинейной образующей). Все касательные плоскости косой Л. п. образуют семейство плоскостей, зависящее от двух параметров.
Важными видами косых Л. п. являются: 1) цилиндроид, образованный движением прямой линии, остающейся перпендикулярной к нек-рому заданному направлению. Цилиндроид может быть определен заданием двух направляющих линий, по к-рым должна скользить образующая, и направляющей плоскостью, к-рой образующая остается параллельной при своем движении. 2) Коноиды, образуемые движением прямой линии, остающейся параллельной заданной плоскости и пересекающей данную прямую. Коноиды представляют собой, т. о., частный случай цилиндроидов.
Лит.: Фиников С. П., Теория поверхностей, М. ― Л., 1934.