Квадратная или тетрагональная система — совокупность кристаллов, у которых можно найти одну (не более) четверную ось простой или сложной симметрии (см. Кристаллографические системы). Кроме одной четверной оси, обязательной для этой системы, может встречаться и большее число элементов симметрии: оси симметрии меньшего порядка (двойные), плоскости простой и сложной симметрии, центр симметрии. Четверная ось принимается за главную кристаллическую ось и обозначается буквою с; две взаимно перпендикулярные и перпендикулярные к оси с двойные оси назыв. боковыми кристаллич. осями; они между собою равны, но больше или меньше главной оси, и обе обозначаются буквою а [1]. Главные и боковые оси совмещаются с координатными (прямоугольными) осями. Кристалл, грани которого пересекают все три координатные оси и при этом две боковые (X и У) на одинаковом расстоянии от начала координат, образует так назыв. основную форму; обозначение ее по Миллеру (111), по Науману Р. Плоскость, в которой лежат боковые оси, следовательно, перпендикулярная главной с, называется базисом или базопинакоидом и обозначается 001 по Миллеру и 0Р по Науману. С общим характером симметрии кристаллов К. системы тесно связано распределение в них различных физических свойств. Так, напр., соответственно существованию здесь единственной (четверной) оси симметрии, которая принимается за главную кристаллическую ось, имеется только одно направление, по которому двойного лучепреломления (см. Двойное лучепрел.) не происходит; оно совпадает с главною осью с. Таким образом, кристаллы К. системы одноосны. Характер теплопроводности (см.), подобно скорости распространения света, может быть представлен в виде сфероида, у которого осью вращения служит главная ось; вследствие этого на плоскостях, перпендикулярных к главной оси, теплопроводность выражается кругом, на других же — эллипсом, что наглядно было доказано Сенармоном фигурами плавления. Расширение при нагревании подчиняется тому же общему характеру: по направлению главной оси (и только главной) один (наибольший или наименьший) коэффициент расширения, по всем другим направлениям — другой, одинаковый для всех направлений, имеющих одинаковый угол с главной осью. Смотря по тому, какие присутствуют еще элементы симметрии, кроме четверной оси симметрии, К. систему подразделяют на семь классов, или отделений, которым даются особые названия.
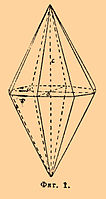
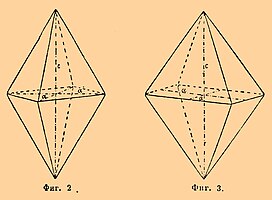
1) Голоэдрия К. системы заключает в себе кристаллы наиболее симметрического расположения граней. В них имеется: четверная ось; четыре двойных оси, делающие между собою угол в 45° и лежащие в плоскости, перпендикулярной к четверной оси; центр симметрии; пять плоскостей симметрии, проходящих через оси симметрии, — четыре пересекаются между собою по четверной оси (главная ось), а пятая — к ним перпендикулярна. Сюда относятся: дитетрагональная бипирамида (осьмигранная двойная пирамида, фиг. 1). Все три параметра каждой плоскости различны и выражаются общим видом a:b:c. Ограничена 16 равными треугольными гранями. Общий знак по Миллеру (hkl) и по Науману mPn. Тетрагональная бипирамида (квадр. пирамида) 1-го рода (фиг. 2). Параметры по боковым осям одинаковы, по главной — больше или меньше; общий вид — а:с. Ограничена 8 равными равнобедренными треугольниками (обозначение hh1 и mP). Тетрагональная бипирамида (квадр. пирамида) 2-го рода по виду совершенно подобна таковой же 1-го рода; отличить их друг от друга можно только тогда, когда они встречаются вместе; в этом случае они бывают повернуты относительно друг друга на 45°, при таком положении боковые оси у бипирамиды 2-го рода пройдут через середины горизонтальных ребер (фиг. 3). Знак: hol и mP∞. Соответственно трем видам бипирамид имеются формы открытия, у которых стороны параллельны главной оси с; они назыв. призмами: дитетрагональная (осмигранная) призма — знак (hko) и ∞Pn (фиг. 4); тетрагональная призма 1-го и 2-го рода, отличающиеся друг от друга тем же, чем отличаются соответствующие бипирамиды (фиг. 5 призма 1-го рода). Наконец, последняя форма того же отдела — две параллельные между собою плоскости базиса, или базопинакоида (см. фиг. 4 и 5 о); знак (001) и оР.
|
|

|
2) Пирамидальная (бипирамидальная) гемиэдрия. Имеется четверная ось симметрии и к ней перпендикулярная плоскость симметрии. Формы, сюда относящиеся, можно вывести из форм первого класса, если представить, что в дитетрагональной пирамиде остаются и по очереди исчезают пары плоскостей, пересекающиеся в средних ребрах. Таким образом, получается форма, совершенно подобная пирамиде 1-го и 2-го рода, но отличающаяся от них положением в пространстве: в ней боковые оси соединяют точки, лежащие не на середине боковых ребер; она называется кв. бипирамидой 3-го рода; знак π(hkl) и π(mPn)/2. Поступая таким же образом с другими голоэдрическими формами (находя в них соответствующие целые плоскости или части плоскостей), мы получим только из дитетрагональной призмы новую форму, призму 3-го рода, совершенно подобную призме 1-го и 2-го рода, но отличающуюся от них положением в пространстве (как в пирамиде 3-го рода); знак π(hko) и ![]() . Все остальные голоэдрич. формы по этому типу гемиэдрии не дают новых форм.
. Все остальные голоэдрич. формы по этому типу гемиэдрии не дают новых форм.
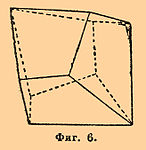
3) Трапецоэдрическая гемиэдрия. Имеются: четверная ось симметрии и четыре двойные оси симметрии, пересекающиеся между собою под углом в 45° и лежащие в плоскости, перпендикулярной к первой. Сюда принадлежит квадратн. трапецоэдр (фиг. 6), который можно получить из дитетрагональной пирамиды путем развития и исчезновения плоскостей, лежащих попеременно. Остальные голоэдр. формы по этому способу наружной своей формы не изменяют. Знак трапецоэдра τ(hkl) и (mPn)/2.
|
|
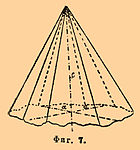
4) Гемиморфия квадратной системы. Одна четверная ось симметрии и четыре плоскости симметрии. Гемиморфные формы могут быть получены из голоэдрических, если допустим развитие их только на одном конце главной оси. Таким путем из дитетрагональной бипирамиды получится простая дитетрагональная пирамида (фиг. 7); бипирамида 1-го и 2-го рода дадут соответствующие пирамиды; наконец, базопинакоид даст только одну плоскость.
5) Гемиморфия гемиэдрии квадр. системы. Только одна четверная ось симметрии.
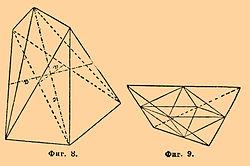
6) Скаленоэорическая гемиэдрия. Характеризуется двумя взаимно перпендикулярными плоскостями симметрии, пересекающимися в одной из трех двойных осей симметрии, которая (ось) является тоже четверной осью сложной симметрии. Две другие двойные оси перпендикулярны к первой и между собою. Формы данного класса могут быть выведены из голоэдрических, если заставить исчезать и развиваться пары плоскостей (в дитетрагональной бипирамиде), отдельных плоскостей (в тетрагональной бипирамиде) и частей плоскостей (в остальных формах), лежащих в так назыв. октантах (пространствах, ограниченных тремя взаимно пересекающимися плоскостями, в которых лежат кристаллические оси). Из дитетрагональной бипирамиды получается скаленоэдр κ(hkl) и (mPn)/2 (фиг. 8); из тетрагональной бипирамиды 1-го рода — квадр. сфеноид κ(hhl) и (mP)/2. Из остальных форм новых не получается.
7) Сфеноидическая тетратоэдрия. Одна четверная ось сложной симметрии и перпендикулярная к ней плоскость сложной симметрии. Сюда принадлежит квадратный сфеноид 3-го рода, который совершенно сходен с квадр. сфеноидом 1-го рода и отличается только своим положением; его плоскости наклонены к кристаллическим осям под различными углами как у осмигранной бипирамиды, но число плоскостей здесь в четыре раза меньше.
Примечания
править- ↑ Кроме того, в кристаллах К. системы можно проводить еще две боковые оси, которые лежат также в плоскости базиса и образуют с упомянутыми боковыми осями угол в 45°. Они назыв. промежуточными осями.