Страница:БСЭ-1 Том 37. Лилль - Маммалогия (1938).pdf/156

очень велика по сравнению с величинами $r$ и $r_{0}$. Введение Л. п. существенно облегчает решение нек-рых задач, сводя их от трехмерного случая к двухмерному.

ЛОГАРИФМЫ. Элементарная теория. Л. данного числа $N$ при основании $a$ называется показатель степени $x$, в к-рую нужно возвести число $a$, чтобы получить $N$. Этот Л. обозначается символом $\log _{a}N$ (иногда $\lg _{a}N$, реже $\mathrm {l} _{a}~N$, $\mathrm {L} _{a}~N$ или $^{\mathrm {a} }\mathrm {log} ~N$). Согласно определению $x=\log _{a}N$, если $N=a^{x}$. Например: т. к. 100=10^{2}, то $\log _{10}100=2$; или т. к. $32=2^{5}$, то $\log _{2}32=5$. Основание Л. $a$ берется положительным, и т. к. при всяком действительном $x$ всегда $a^{x}>0$, то лишь положительные числа имеют действительный Л. Выбор отрицательного основания привел бы к тому, что бесчисленное множество положительных и отрицательных чисел не имело бы действительных Л. Совокупность всех Л., соответствующих основанию $a$, называется системой Л. при основании $a$. Из определения Л. следует, что $a^{\log _{a}N}=N$, с помощью чего легко выводятся главные свойства логарифмов:

1) Л. произведения равен сумме Л. сомножителей: $\log _{a}(MN)=\log _{a}M+\log _{a}N$.

2) Л. частного равен разности Л. делимого и делителя: $\log _{a}({\frac {M}{N}})=\log _{a}M-\log _{a}N$.

3) Л. степени равен произведению показателя степени на Л. возводимого в степень числа: $\log _{a}N^{n}=n\cdot \log _{a}N$, Л. Отсюда вытекает также, что Л. чисел, образующих геометрич. прогрессию, сами составляют арифметическую прогрессию.

4) Л. корня равен Л. подкоренного выражения, деленному на показатель корня:

$\log _{a}{\sqrt[{n}]{N}}={\frac {1}{n}}\log _{a}N.$

Число, Л. которого есть $x$, называют антилогарифмом $x$.

Огромное практическое значение Л. основывается на перечисленных свойствах, позволяющих с помощью специальных таблиц Л. заменять умножение, деление, возведение в степень и извлечение корня соответственно более простыми сложением, вычитанием, умножением и делением.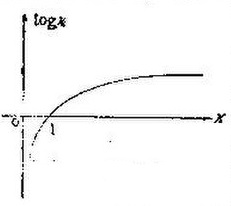Рис. 1. Многие вычисления без Л. были бы почти неосуществимыми. По выражению Лапласа, «логарифмы, сократив труды астронома, удвоили его жизнь». — Благодаря десятичному характеру нашего счета особенно употребительной является система Л. с основанием $10$. Десятичные Л. обозначают обычно $\log N$. На рис. 1 показана зависимость между числами $x$ и их десятичными Л.; видно, что $\log x<0$ при $x<1$, $\log 1=0$ и $\log x>0$ при $x>1$. Ноль не имеет Л. Десятичные Л. чисел, представляющих собой целые степени числа $10$, — сами целые ($\log 10^{n}=n)$; Л. остальных целых чисел суть трансцендентные числа (см. Число) и выражаются бесконечными непериодич. десятичными дробями. В таблицах приводятся поэтому лишь приближенные значения Л. Целую часть Л. называют характеристикой, а дробную — мантиссой. Например у $\log 253=2,40312$ характеристика есть $2$, а мантисса — $0,40312$. Л. чисел, меньших единицы, приводят к специальной форме, в к-рой их мантисса оказывается положительной. Например $\log 0,05={\overline {2}},69897$; это означает, что $\log 0,05=\log 5-\log 100=0,69897$ $-2$. Характеристика Л. числа, большего $1$, равна числу цифр, содержащихся в его целой части, минус единица; например $\log 1000=3$. Характеристика Л. десятичной дроби, меньшей $1$, равна числу нолей, содержащихся в десятичной дроби до первой отличной от ноля цифры, взятому со знаком минус. Мантисса Л. всегда положительна. Для построения таблиц Л. весьма важно также, что числа, отличающиеся в $10^{n}$ раз, имеют одинаковые мантиссы. Поэтому в таблицах можно приводить лишь мантиссы целых чисел. Например, зная, что $\log 253=2,40312$, легко получаем $\log 25,3=1,40312$, $\log 2,53=0,40312$, $\log 0,25=1,40312$ и т. д.

В большинстве случаев практически достаточны таблицы, дающие пять знаков мантиссы; для выкладок, требующих особенной точности, Рис. 2.пользуются семизначными Л. В СССР широко распространены пятизначные таблицы логарифмов Пржевальского. В приведенном образце (рис. 2) содержатся Л. чисел от $2500$ до $2599$, напр. $\log 2511=3,39985$. Для вычисления Л. чисел, состоящих более чем из четырех цифр, служат таблички пропорциональных частей — Р. Р. Таблицы Л. содержат обычно указания, как ими пользоваться. Л. можно пользоваться и при действиях над отрицательными числами, оперируя над их абсолютными величинами и придавая затем результату подходящий знак. Кроме Л. чисел, таблицы содержат обычно Л. тригонометрии, величин и т. н. Гауссовы логарифмы. Гауссовы Л. служат для определения Л. суммы или разности двух чисел по данным их Л. без промежуточного отыскания самих чисел. Нахождение $\log(a+b)$ основывается на формуле

$\log(a+b)=\log a+\log \left[1+{\frac {1}{\left({\frac {a}{b}}\right)}}\right].$

Наряду с десятичными Л. большое значение имеют натуральные Л., основанием к-рых служит трансцендентное число $e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=2,718281828459...$; их обозначают $\ln N$. Натуральные Л. служат и в практич. вычислениях, но особенно существенны они в теории функций (см. ниже). Натуральные логарифмы называют также гиперболическими, ибо площадь $S$, ограниченная дугой равносторонней гиперболы $y={\frac {1}{x}}$ (рис. 3), отнесенной к асимптотам, осью абсцисс и ординатами, соответствующими абсциссам $1$ и $x$, равна $\ln x$.

Зная Л. какой-либо одной системы, можно получить легко Л. любой другой. Прологарифмировав в системе с основанием $b$ тождество