Начертательная геометрия — наука, изучающая пространственные фигуры при помощи их проектирования (проложения) на некоторые плоскости. Способов проектирования может быть несколько. Напр., представим себе, что в точке O (рис. 1) находится глаз человека, смотрящего на предмет AB.
Рис. 1. Вообразим между глазом и предметом плоскость MN. Проведем из O прямые к тем точкам предмета, которые характеризуют его форму. Эти прямые, называемые проекционными лучами, пересекут плоскость MN в различных точках. Совокупность таких точек ab и составит картину предмета AB, служащую его изображением. Поэтому плоскость MN и называется плоскостью картины. Точка пересечения проекционного луча и плоскости картины называется центральною проекциею или перспективою той точки предмета, из которой исходит данный проекционный луч. Такой способ изображения предмета называется перспективою. 
Рис. 2. Если вместо того, чтобы проводить проекционные лучи от точек предмета к глазу, мы будем опускать перпендикуляры из точек предмета на плоскость картины, то полученное изображение, представляемое совокупностью оснований этих перпендикуляров, будет сохранять некоторое сходство с перспективным. Действительно, чем более точка O будет удалена от предмета, тем более проекционные лучи будут приближаться к положению взаимно параллельному и перпендикулярному к плоскости картины. Такое изображение называется ортогональною проекциею. Итак, в ортогональной проекции каждая точка предмета изображается основанием перпендикуляра, опущенного из нее на плоскость картины. Получение, по данному чертежу, истинных размеров и другие построения несравненно проще выполняются при ортогональном проектировании, чем при перспективе. Основная идея Н. геометрии заключается в следующем: если имеются две ортогональные проекции предмета на две плоскости, различным образом относительно предмета расположенные, то, помощью сравнительно несложных построений над этими двумя изображениями, можно получить истинные размеры предмета, истинный вид его плоских линий и ортогональную проекцию на любую заданную третью плоскость. Конечно, для этого необходимо нужно знать, в каком масштабе были даны заданные две ортогональные проекции, т.-е., в каком общем отношении весь чертеж был уменьшен или увеличен против действительности. Обыкновенно задают вид предмета его 
Рис. 3.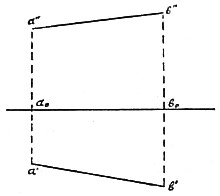
Рис. 4. ортогональными проекциями на такие две плоскости, из которых одна горизонтальна и называется планом, а другая вертикальна и называется фасадом. Их также называют горизонтальною и вертикальною плоскостями проекций. Ортогональная проекция предмета на плоскость, перпендикулярную к плану и фасаду, называется боковым видом. Весьма важный прием Н. геометрии заключается в том, что плоскость фасада, бокового вида и всякие другие плоскости, на которые проектируется предмет, мысленно отгибают на плоскость плана поворотом около прямой, по которой план пересекается с отгибаемою плоскостью. Этот прием называется совмещением. Дальнейшие построения совершаются уже на таком совмещенном чертеже, как это указано ниже. — Так как всякий предмет представляет собою совокупность точек, то прежде всего необходимо познакомиться с изображением плана и фасада точки на совмещенном чертеже. Пусть a (рис. 2) будет данная точка; P — плоскость плана; Q — плоскость фасада. Опустив из a перпендикуляр на план, получим план a′ точки a; опустив из a перпендикуляр на фасад, получим фасад b точки a. Перпендикуляры aa′ и ab называются проектирующими линиями. Плоскость baa′, определяемая проектирующими линиями, называется проектирующею плоскостью. Она перпендикулярна как плану, так и к фасаду и, следовательно, перпендикулярна к пересечению плоскости плана и фасада, называемому общим прорезом. 
Рис. 5. Пусть a0 есть та точка, в которой проектирующая плоскость пересекается с общим прорезом: a0a′ и a0b будут перпендикулярны к общему прорезу. При данных плоскостях плана и фасада положение точки a вполне определяется ее планом a′ и фасадом b, так как a находится на пересечении перпендикуляра, восстановленного из a′ к плоскости плана, с перпендикуляром, восстановленным из b к плоскости фасада. Для получения совмещенного чертежа повернем плоскость Q фасада в направлении, указанном стрелкою, около общего прореза до совпадения с плоскостью плана. При этом точка b упадет в a″. Таким образом точка a″, представляющая собою совмещенный фасад точки a, будет лежать на продолжении перпендикуляра a′a0, опущенного из плана a′ на общий прорез. Таким образом получится совмещенный чертеж, изображенный на рис. 3, где MN есть общий прорез; a′ — план и a″ — совмещенный фасад точки a, которая сама уже не изображается.Проекция прямой.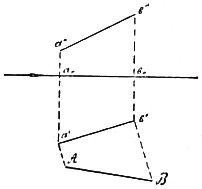
Рис. 6. Н. геометрия имеет дело только с совмещенными чертежами; каждая точка дается планом и совмещенным фасадом; к чертежам же, исполненным обыкновенными приемами (каковы у нас рис. 1, 2 и 5), прибегают только в начале изучения этой науки. Прямая определяется двумя точками. Следовательно, если имеется план и фасад (совмещенный) двух точек a и b, лежащих на прямой, то прямая a′b′, соединяющая планы точек a и b, будет планом прямой ab, и прямая a″b″, соединяющая фасады точек a и b, будет фасадом прямой ab. На чертеже 4 изображена прямая ab своими планом и фасадом. Определение истинной длины прямолинейного отрезка, заданного планом и фасадом. Воспользуемся чертежом, исполненным обыкновенным способом (рис. 5). Пусть ab есть данный прямолинейный отрезок, a′b′ его план, a″b″ его фасад. Повернем плоскость a′abb′ около прямой a′b′ и отогнем ее в положение a′b′BA на плоскость плана. При этом отрезок ab примет положение AB. Следовательно:
Перпендикулярность прямых a′a и b′b к a′b′ не изменилась; следовательно, чтобы по данному плану и фасаду прямолинейного отрезка на совмещенном чертеже (рис. 6) определить истинную его длину, нужно восставить из a′ и b′ к плану a′b′ перпендикуляры и на них отложить a′A = a0a″; b′B = b0b″. Прямая AB и будет равна истинной длине прямой ab. На этом примере и видим, что на чертеже 5, исполненном обыкновенным способом, прямая ab изображена в укороченном виде соответственно тому, как мы ее видим, и так как степень этого укорочения неизвестна, то по чертежу 5 нельзя определить истинного расстояния ab. Между тем, на чертеже 6, хотя сама прямая ab и не изображена, а даны только ее план a′b′, и фасад a″b″, можно по ним совершенно точно определить представляемую ими прямую. Подобным же образом изучение всяких пространственных фигур может быть произведено при помощи их проекций. Н. геометрия создана была в конце XVIII столетия Монжем. Она имеет тесное отношение к теории теней и к способу аксонометрических проекций. — Лучшими руководствами по Н. геометрии могут служить курсы: Н. И. Макарова (1903, 4-е изд.), Сомова, Monge, Leroy.