БСЭ1/Эволюта и эвольвента

Эволюта и эвольвента
Большая советская энциклопедия (1-е издание)

Словник: Э — Электрофон. Источник: т. LXIII (1933): Э — Электрофон, стлб. 52—53 ( РГБ )

ЭВОЛЮТА И ЭВОЛЬВЕНТА, плоские кривые, находящиеся в следующем соотношении друг с другом: представим себе нек-рую кривую C (рис. 1), на к-рую намотана нить; 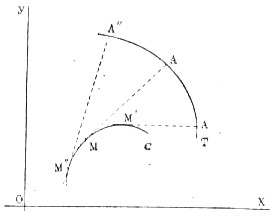Рис. 1. в точке M эта нить отведена по касательной MA; если мы будем теперь сматывать эту нить с кривой C, оставляя ее натянутой, то точка A будет описывать нек-рую кривую T, которая и называется эвольвентой кривой C; сама же кривая C по отношению к кривой T называется эволютой (построение Эйлера). — Примеры. Эволюта окружности вырождается в одну точку — центр окружности; эвольвента окружности — спираль (рис. 2а). Эволюта эллипса есть астроида (рис. 2б). Эволюта циклоиды есть снова циклоида, равная первой, но смещенная относительно нее вдоль оси x на расстояние π (рис. 2в). — Более строго понятия Э. и э. определяются так: эволюта C кривой T (эвольвенты) есть огибающая (см.) Рис. 2. всех нормалей кривой T, или геометрическое место всех ее центров кривизны (см.). Длина дуги эволюты C равна разности радиусов кривизны эвольвенты T, соответствующих концам этой дуги.

Аналитически определение эвольвенты по эволюте разрешается интегрированием дифференциального уравнения

${\frac {d\varrho }{dt}}+{\frac {\varphi '\varphi ''+\psi '\psi ''}{\varphi '^{2}+\psi '^{2}}}\varrho +1=0,$

(1)

где x = φ(t), у = ψ(t) суть ур-ия эволюты, а величина ϱ определяет положение точки эвольвенты (ξ, η) на касательной к эволюте: ξ = φ + ϱφ’; η = ψ + ϱψ’. Особый интерес представляет эвольвента круга (рис. 2а и 3), обладающая рядом замечательных геометрических свойств. Полагая в ур-ии (1) φ = a sin t, ψ = a cos t и интегрируя его, получаем для эвольвенты круга ур-ие

$\xi =a(\cos t+t\sin t)$;          $\eta =a(\sin t-t\cos t)$.

(2)

Если через R обозначить радиус кривизны эвольвенты круга, а через S длину ее дуги, то R²=2aS.

Рис. 3. Понятие об эвольвенте плоской кривой может быть перенесено на пространственные кривые. Кривая С есть эволюта кривой T, если касательные кривой C являются нормалями кривой T. Можно показать, что всякая кривая T имеет ∞¹ эволют. Все эти эволюты могут быть получены из одной из них (C) путем поворота на постоянный угол около соответствую­щих точек кривой T в нормальных ее плоскостях, касательных к кривой C. Дальнейшим обобщением понятия эволюты служит понятие о поверхностях центров данной поверхности.

Лит.: все курсы дифференциального исчисления и дифференциальной геометрии, например Гурса Э.; Курс математиче­ского анализа, т. I, Москва, 1911, гл. 10; Егоров Д. Ф., Дифференциальная геометрия, М.—Л., [1924]; Loria G., Spezielle algebraische und transzendente ebene Kurven, В. II, 2 Aufl., Lpz., 1911; Scheffers G., Anwendung d. Differential- und Integral-Rechnung auf Geometrie, Band I — Einführung in die Theorie der Kurven in der Ebene und im Räume, 3 Auflage, Berlin, 1923.