БСЭ1/Логарифмическая спираль

Логарифмическая спираль
Большая советская энциклопедия (1-е издание)

Словник: Лилль — Маммалогия. Источник: т. XXXVII (1938): Лилль — Маммалогия, стлб. 298 ( РГБ )

ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ, кривая линия, к-рая пересекает под одним и тем же (острым) углом все прямые, выходящие на плоскости из некоторой точки («полюс Л. с.»).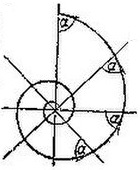 При этом, как всегда, под углом между прямой линией и кривой подразумевают угол между этой прямой и касательной, проведенной к кривой линии в точке ее пересечения с прямой. Л. с. имеет вид незамкнутой кривой, образующей бесконечное множество завитков вокруг своего полюса. Точка, движущаяся по спирали, в одном направлении будет неограниченно удаляться от полюса, в другом — неограниченно приближаться к полюсу, никогда его не достигая. В полярных координатах $(r,\varphi )$ уравнение Л. с. может быть приведено к виду $r=c^{\varphi }$, где $c$ — положительное постоянное число. Отсюда видно, что если угол $\varphi$ изменяется в арифметич. прогрессии, то радиус-вектор $r$ изменяется в геометрич. прогрессии. Иначе: полярный угол $\varphi$ изменяется пропорционально логарифму расстояния $(r)$ точки от полюса (отсюда название кривой). — Формулированное в самом начале свойство логарифмической спирали находит себе применение в технике: при устройстве фрезера постоянство «угла резания» достигается тем, что зубцы фрезы затачиваются в форме дуг логарифмической спирали.